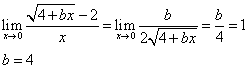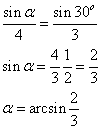
Per il teorema dei seni si ha
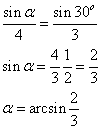
Poiché angoli supplementari hanno seni uguali, i possibili valori approssimati di α sono:
Se la figura proposta implica che α deve essere acuto, l'unico valore accettabile è il primo.
Il quesito è ricorrente nelle prove d'esame PNI. Si veda 2009 -quesito 4 e 2006 - quesito 2.
In un poliedro regolare gli angoli delle facce aventi vertice in comune devono essere almeno 3, devono essere congruenti e la loro somma deve essere minore di un angolo giro. Gli angoli interni di un esagono regolare misurano 120°, dunque non può esistere un solido regolare (o "platonico") con facce esagonali.
La probabilità che la prima pallina estratta sia rossa è 5/20.
La probabilità che la seconda pallina non sia rossa è 15/19.
La probabilità che la terza pallina non sia rossa è 14/18.
La probabilità di questa sequenza di eventi è
![]()
Dato che la pallina rossa può essere estratta anche come seconda o come terza, il risultato precedente va moltiplicato per 3. Dunque la probabilità che solo una delle palline estratte sia rossa è
![]()
La probabilità che tre palline abbiano colore diverso è
![]() .
.
I tre colori possono presentarsi in 3!=6 ordini diversi e le combinazioni di 4 colori a gruppi di 3 sono
![]() .
.
Dunque la probabilità di estrarre gruppi di tre palline di diverso colore è
![]()
Il volume richiesto è dato dall'integrale
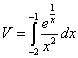
Per il calcolo, conviene cambiare la variabile di integrazione nel seguente modo
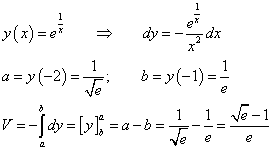
Un quesito analogo è stato proposto anche nell'esame del 2007 - quesito 5.
Un semplice modello di geometria non euclidea sferica può essere rappresentato da una superficie sferica, che ha lo stesso ruolo di un piano nella geometria euclidea, nella quale si connotano come 'rette' le circonferenze massime.
È evidente che due circonferenze massime hanno sempre due punti in comune, quindi in questo modello, data una 'retta' e un punto esterno ad essa, per questo punto non passa nessuna 'retta' parallela a quella considerata e non vale quindi l'affermazione nota come quinto postulato di Euclide.
Se si considerano sulla superficie due punti diametralmente opposti, come, ad esempio, i poli sulla superficie terrestre supposta perfettamente sferica, due circonferenze massime passanti per questi punti, come, ad esempio, due meridiani, e l'equatore rispetto ai poli scelti, le intersezioni tra due meridiani distinti e l'equatore delimitano un triangolo sferico 'isoscele' in cui gli angoli alla base sono entrambi retti. Nella somma degli angoli interni bisogna aggiungere anche l'angolo con vertice in un polo e quindi la somma degli angoli interni risulta maggiore di un angolo piatto.
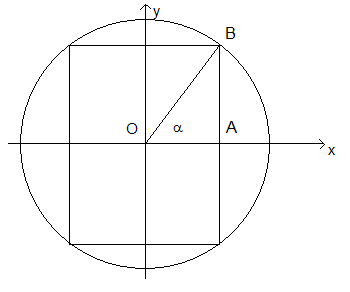
Si suppone che il massimo cilindro del testo sia il cilindro di volume massimo.
Si rappresenta una sezione piana della costruzione in un sistema cartesiano ortogonale con origine nel centro O della sfera e asse delle ordinate coincidente con l'asse del cilindro inscritto.
Detto α l'angolo AOB, il segmento OA misura √3 cosα e il segmento AB misura √3 sinα. Il volume del cilindro in funzione di α risulta
![]() con
con ![]() .
.
Derivando e semplificando, si ottiene
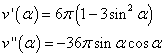
Nell'intervallo considerato, la derivata prima si annulla per
![]() da cui
da cui
![]() .
.
Per questi valori la derivata seconda risulta negativa, quindi il volume risulta massimo. Si ottiene quindi
![]() e
e
![]()
Per approssimare gli zeri della derivata prima proposta, conviene interpretarli come le ascisse delle intersezioni tra i grafici delle funzioni
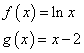
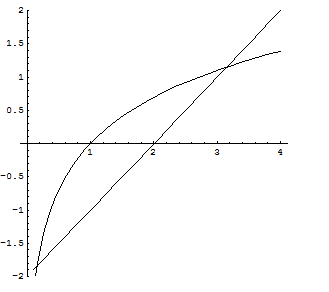
Tra i valori proposti, sono ammissibili il D e il B. Calcolando il valore della derivata seconda
![]() nei due casi, essa risulta positiva solo
nel caso D.
nei due casi, essa risulta positiva solo
nel caso D.
Enumerando tutte le terne che sommano 9 si ha
| ordinale | 1° dado | 2° dado | 2° dado |
|---|---|---|---|
| 1 | 1 | 2 | 6 |
| 2 | 1 | 3 | 5 |
| 3 | 1 | 4 | 4 |
| 4 | 1 | 3 | 3 |
| 5 | 1 | 6 | 2 |
| 6 | 2 | 1 | 6 |
| 7 | 2 | 2 | 5 |
| 8 | 2 | 3 | 4 |
| 9 | 2 | 4 | 3 |
| 10 | 2 | 5 | 2 |
| 11 | 2 | 6 | 1 |
| 12 | 3 | 1 | 5 |
| 13 | 3 | 2 | 4 |
| 14 | 3 | 3 | 3 |
| 15 | 3 | 4 | 2 |
| 16 | 3 | 5 | 1 |
| 17 | 4 | 1 | 4 |
| 18 | 4 | 2 | 3 |
| 19 | 4 | 3 | 2 |
| 20 | 4 | 4 | 1 |
| 21 | 5 | 1 | 3 |
| 22 | 5 | 2 | 2 |
| 23 | 5 | 3 | 1 |
| 24 | 6 | 1 | 2 |
| 25 | 6 | 2 | 1 |
Si hanno 25 possibili terne, ognuna con probabilità 1/6*1/6*1/6, quindi la probalità di totalizzare 9 è
![]()
Le terne che sommano 10 sono
| ordinale | 1° dado | 2° dado | 2° dado |
|---|---|---|---|
| 1 | 1 | 3 | 6 |
| 2 | 1 | 4 | 5 |
| 3 | 1 | 5 | 4 |
| 4 | 1 | 6 | 3 |
| 5 | 2 | 2 | 6 |
| 6 | 2 | 3 | 5 |
| 7 | 2 | 4 | 4 |
| 8 | 2 | 5 | 3 |
| 9 | 2 | 6 | 2 |
| 10 | 3 | 1 | 6 |
| 11 | 3 | 2 | 5 |
| 12 | 3 | 3 | 4 |
| 13 | 3 | 4 | 3 |
| 14 | 3 | 5 | 2 |
| 15 | 3 | 6 | 1 |
| 16 | 4 | 1 | 5 |
| 17 | 4 | 2 | 4 |
| 18 | 4 | 3 | 3 |
| 19 | 4 | 4 | 2 |
| 20 | 4 | 5 | 1 |
| 21 | 5 | 1 | 4 |
| 22 | 5 | 2 | 3 |
| 23 | 5 | 3 | 2 |
| 24 | 5 | 4 | 1 |
| 25 | 6 | 1 | 3 |
| 26 | 6 | 2 | 2 |
| 27 | 6 | 3 | 1 |
Si hanno 27 possibili terne, ognuna con probabilità 1/6*1/6*1/6, quindi la probalità di totalizzare 9 è
![]()
Anche questo quesito è ricorrente negli esami PNI. Si veda, ad esempio, 2013 - quesito 9.
L'insieme Q dei razionali è equipotente all'insieme N dei naturali: è quindi un insieme numerabile con cardinalità ℵ0, mentre l'insieme R dei reali ha la potenza del continuo, che, come dimostrato da G. Cantor, ha cardinalità superiore ad ℵ0.
Per una trattazione più dettagliata, ma sicuramente eccedente la sintesi necessaria nella risposta ad un quesito d'esame, si può vedere Wikipedia.
Assumendo non negativo il radicando a numeratore, il limite può sussistere solo se anche il numeratore tende a 0, cioè se
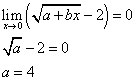
Applicando il teorema di De L'Hôpital, si ha