(a cura di Roberto Bigoni)
Quando due oggetti del pensiero a e A sono collegati da una relazione di appartenenza (indicata usualmente con il simbolo ∈, detto "simbolo di Peano")
![]()
a è detto elemento dell'insieme A.
L'insieme A può essere individuato in modo estensivo, cioè elencando tra graffe tutti gli elementi che appartengono ad A.
Esempio:
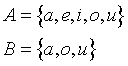
Nell'esempio si nota che tutti gli elementi di B sono anche elementi di A. Quando si verifica questa situazione si dice che B è un sottinsieme di A.
![]()
Se, come nel caso proposto, c'è almeno un elemento di A che non appartiene a B, si dice che B è un sottinsieme proprio di A
![]()
Ma spesso ci si trova nell'impossibilità pratica o teorica di elencare tutti gli elementi di un insieme e risulta quindi molto più efficace e generale individuare gli insiemi in modo intensivo, enunciando cioè una proprietà che, se posseduta da un elemento, equivale alla dichiarazione di appartenenza.
Questa proprietà è espressa da una funzione logica p(x), cioè da una proposizione dichiarativa costituita da un soggetto variabile x (argomento della funzione) e da un predicato p applicabile al soggetto x, tale da risultare vera o falsa a seconda del valore di x.
Il predicato p definisce implicitamente i soggetti x ai quali esso può essere sensatamente applicato. L'insieme U di questi oggetti è l'insieme universo della funzione logica.
Dato il predicato p, l'universo U viene suddiviso in due sottinsiemi:
l'insieme P formato da tutti e soli gli elementi che rendono vera la frase “ x è p”
![]()
che si interpreta : “P è l'insieme di tutte le x tali che p(x) è vera.”;
P è detto insieme di verità della funzione p(x);
l'insieme formato da tutti e soli gli elementi che rendono falsa la frase “ x è p”
questo è l'insieme di falsità di p(x) o insieme complementare di P.
Esempio:
p(x) = “x è una vocale”.
x, il soggetto della dichiarazione, è l'argomento della funzione logica; 'è una vocale' è il predicato.
![]()
Se a x si attribuisce il valore i si ottiene una proposizione vera, mentre se a x
si attribuisce il valore s si ottiene una proposizione falsa.
Se però a x si attribuisce il valore 1 si ottiene una frase senza senso, di cui non si può dire se è vera o
falsa. Il numero 1 non appartiene all'universo di p(x). Nell'esempio, l'universo è ovviamente l'alfabeto.
L'insieme complementare di P, che può essere indicato sopralineando P, è l'insieme di verità della negazione di p(x), indicata con –p(x), da leggere “non è vero che…” seguita dall'enunciato p(x).
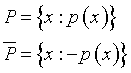
Nell'esempio proposto, l'insieme di falsità è l'insieme delle consonanti.
Esempio: p(x)=”x è una vocale”.
p(“e”): Vero.
p(“s”): Falso.
–p(“s”): Vero.
–(-p(“a”)): Vero.
Esempio di complementare con WolframAlpha.
Una funzione logica che non è verificata da nessun elemento dell'universo ha come insieme di falsità il l'universo stesso. Le si attribuisce come insieme di verità l'insieme vuoto, denotato solitamente con ∅.
Esempio.
p(k)=”k è un mese di 32 giorni”.
È chiaro che l'universo è l'insieme M dei mesi dell'anno.
Ogni elemento di M falsifica la p(k).
L'insieme di verità di p(k) è ∅.
L'insieme di verità di -p(k) è M.
Gli insiemi studiati in matematica sono quasi esclusivamente insiemi infiniti, impossibili da rappresentare
esaustivamente in modo estensivo. Talora, per individuare intuitivamente un insieme, se ne elencano alcuni elementi,
terminando l'elenco con dei puntini di ellissi …. Ad esempio, l'insieme P dei numeri pari
può essere rappresentato come P={2,4,6,8,10,…}. In questo modo il lettore è in grado di capire di
che insieme si parla solo se, dagli elementi elencati, è in grado di congetturare una rappresentazione intensiva dell'insieme,
applicando più o meno consapevolmente il di principio induzione matematica.
In linea di massima è quindi preferibile usare direttamente una rappresentazione intensiva. Ad esempio, considerato noto l'insieme dei numeri naturali N, l'insieme dei numeri pari si può definire nel seguente modo:
![]()
Usando l'operatore Range di Mathematica utilizzabile in
WolframAlpha si può ottenere una rappresentazione estensiva di un numero a piacere
di elementi di P:

Quando si può dire che un insieme è infinito? Una prima risposta, valida ad esempio per l'insieme dei numeri naturali (ma anche per l'insieme dei numeri pari o per l' insieme di numeri primi) potrebbe essere: "Un insieme è infinito se è impossibile trovare il massimo o il minimo dei suoi elementi".
Questa definizione però può funzionare solo per insiemi ordinati e neanche per tutti. Ad esempio non funzionerebbe per l'insieme dei numeri reali x tali che 0≤x≤1. Tanto meno sarebbe applicabile ad insiemi non ordinati, come l'insieme dei numeri complessi.
Una risposta, ritenuta ancor oggi sostanzialmente, valida venne data forse per primo da Galileo: un insieme è infinito se è equipotente ad un suo sottinsieme proprio. Si veda, ad esempio, la definizione di insieme infinito proposta in Wikipedia.
Esempio.
L'insieme N dei numeri naturali è equipotente all'insieme P dei numeri pari, che è un suo insieme proprio, in quanto ad ogni n∈N si può far corrispondere uno e un solo elemento di P, ad esempio 2n. Dunque l'insieme N è infinito.
Date due funzioni logiche p(x) e q(x) con identico universo e con insiemi di verità P e Q, la funzione logica c(x) che è vera solo per gli argomenti che verificano entrambe le funzioni è detta congiunzione (o anche prodotto logico) di p(x) e q(x).
Questa funzione si indica solitamente interponendo tra le due funzioni il simbolo ∧ che si legge
“e” all'italiana o “et” alla latina o “and” all'inglese. Sono in uso anche i simboli &
o i simboli di moltiplicazione (compreso il semplice accostamento).
![]()
L'operatore binario ∧ (o uno dei suoi equivalenti) è detto connettivo di congiunzione.
L'insieme di verità C di c(x) è detto insieme intersezione (o, semplicemente, intersezione) di P e Q:
![]()
Esempio.
Le due funzioni logiche p(k)=”k è pari” e q(k)=”k è multiplo di 3” hanno entrambe come universo l'insieme N dei numeri naturali. Detto P l'insieme di verità di p(k) e Q l'insieme di verità di q(k),
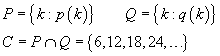
Esempio di intersezione con WolframAlpha.
Se nel dominio nessun elemento verifica la congiunzione, l'intersezione è vuota.
Esempio.
p(k)=”k è pari”; q(k)=”k è dispari”
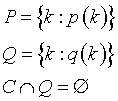
In seguito, quando si connettono due funzioni, si assume implicitamente che abbiano ugual dominio.
Date due funzioni logiche p(x) e q(x) con identico universo e con insiemi di verità P e Q,
la funzione logica d(x) che è vera solo per gli argomenti che verificano almeno una delle due (eventualmente entrambe)
è detta disgiunzione inclusiva (o anche somma logica) di p(x) e q(x).
Questa funzione si indica interponendo tra le funzioni date il simbolo ∨ che si legge “o” all'italiana o
“vel” alla latina o “or”
all'inglese. Sono in uso anche i simboli | o +.
![]()
L'operatore binario ∨ (o uno dei suoi equivalenti) è detto connettivo di disgiunzione.
L'insieme di verità D di d(x) è detto insieme unione (o, semplicemente, unione) di P e Q
![]()
Esempio.
Riprendendo le due funzioni p(x) e q(x) del primo degli esempi precedenti e i loro insiemi di verità P e Q, indicando estensivamente alcuni elementi dell'insieme D si ha D={1,2,3,4,5,6,7,8,9,10,...}
Esempio di unione con WolframAlpha.
Date due funzioni logiche p(x) e q(x) con identico universo e con insiemi di verità P e Q, la funzione logica i(x) che è vera solo per gli argomenti per cui non è vero che verificano la prima ma non la seconda è detta implicazione materiale tra p(x) e q(x). Questa funzione si indica interponendo tra le funzioni date il simbolo → che si legge “implica”.
![]()
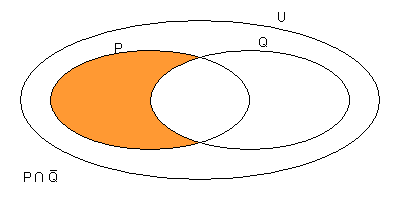
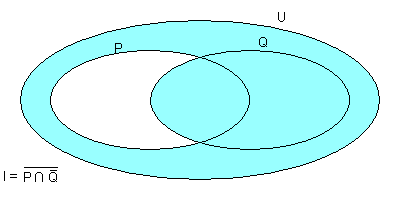
L'insieme di verità I di i(x) include Q ma non P. Si scrive
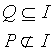
e si legge “Q è sottinsieme di I”, “P non è un sottinsieme di I”.
Esempio.
Riprendendo le due funzioni logiche p(x) e q(x) degli esempi precedentemente proposti (p(k)=”k è pari” e q(k)=”k è multiplo di 3”) e i loro insiemi di verità P e Q, l'insieme I di tutti gli elementi di N che verificano l'implicazione tra p(x) e q(x) è
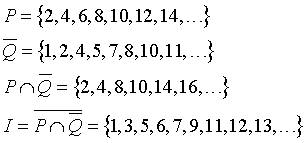
Allora
p(1) → q(1) : Vero (“1 è pari implica che 1 è multiplo di 3”: una falsità implica qualunque cosa, vera o false che sia)
Con WolframAlpha.
p(2) → q(2) : Falso (“2 è pari implica che 2 è multiplo di 3”: una verità non può implicare una falsità).
Con WolframAlpha.
Se I coincide con l'universo, P è un sottinsieme di Q.
Esempio.
p(x)=”x è un quadrato”, q(x)=”x è un rettangolo”.
Ovviamente l'universo è l'insieme delle figure geometriche piane.
La congiunzione
![]()
risulta vera solo per i quadrati che non sono rettangoli. Tali quadrati non esistono. La congiunzione è sempre falsa e la sua negazione sempre vera. Quindi P⊂Q.
Dati (nello stesso universo) due insiemi P e Q:
la loro intersezione è un sottinsieme della loro unione;
questo si assume vero anche se l'intersezione è vuota, quindi l'insieme vuoto è sottinsieme di tutti gli insiemi;
intersezione e unione sono commutative:
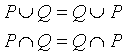
l'intersezione è distributiva rispetto all'unione e viceversa:
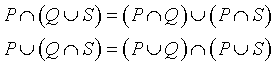
l'unione di un insieme con un suo sottinsieme dà l'insieme; l'intersezione di un insieme con un suo sottinsieme dà il sottinsieme (leggi di assorbimento)
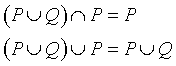
prime leggi di De Morgan
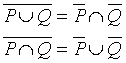
Ad ognuna di queste proprietà degli insiemi corrisponde un'analoga proprietà delle funzioni logiche che li definiscono.
Ad esempio, le leggi di De Morgan in logica diventano
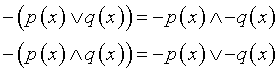
In lingua:
Si lascia all'esercitazione personale la formulazione logica delle altre proprietà.
Per le leggi di De Morgan l'implicazione materiale può essere definita anche nel seguente modo
![]()
Per affermare che una funzione logica p(x) è verificata da tutti gli elementi dell'universo X, soprattutto se X è infinito, è utile introdurre il quantificatore universale ∀ che si legge “per ogni”
![]()
“Per ogni x, p(x)”.
Traducendo in lingua corrente: “L'affermazione p(x) è sempre vera”.
Quantificatore universale con WolframAlpha.
L'uso del quantificatore universale e dell'implicazione materiale può essere sintetizzato dal connettivo di implicazione logica ⇒ (che si legge “se…allora…”)
![]()
Esempio.
Se l'universo è l'insieme dei triangoli e se b(x)=”x è equilatero” e a(x)=”x è isoscele”, l'interpretazione di
![]()
è “Se un triangolo è equilatero allora è isoscele”. Nel linguaggio insiemistico: “L'insieme dei triangoli equilateri è un sottinsieme dell'insieme dei triangoli isosceli”.
Per dire che B, insieme di verità di b(x) è un sottinsieme proprio di A, insieme di verità di a(x)
![]()
Esempio.
Con riferimento all'esempio precedente, l'interpretazione di
![]()
è “Tutti i triangoli equilateri sono isosceli, ma non tutti i triangoli isosceli sono equilateri”.
In linguaggio insiemistico: “L'insieme dei triangoli equilateri è un sottinsieme dell'insieme dei triangoli isosceli”.
Per dire che B, insieme di verità di b(x) coincide con A, insieme di verità di a(x), è utile l'introduzione del connettivo di doppia implicazione logica ⇔ (che si legge “…se e solo se…”)
![]()
Esempio.
Se l'universo è l'insieme dei triangoli e a(x)=”x ha due lati uguali” e b(x)=”x ha due angoli uguali”, l'interpretazione di
![]()
è “Un triangolo ha due angoli uguali se e solo se ha due lati uguali”.
In linguaggio insiemistico: “L'insieme dei triangoli con due angoli uguali coincide con l'insieme dei triangoli con due lati uguali”.
Per affermare che nell'universo X almeno un elemento verifica la proposizione p(x), si introduce il quantificatore esistenziale ∃, che si legge “Esiste almeno un”
![]()
“Esiste almeno un elemento x per cui p(x) è vera”.
Traducendo in lingua corrente: “l'affermazione p(x) è vera almeno in un caso”.
Quantificatore esistenziale con WolframAlpha.
Esempio: per dire che l'intersezione tra due insiemi A e B definiti da a(b) e b(x) non è vuota:
![]()
Nell'universo X ={a,b,c,d,…} l'applicazione del quantificatore universale alla funzione logica p(x) afferma che la p(x) è vera per ogni elemento di X, cioè che è vera la congiunzione logica
![]()
La negazione di questa congiunzione, per le prime leggi di De Morgan, equivale alla disgiunzione delle negazioni
![]()
cioè: è vera almeno una delle negazioni.
![]()
Esempio: Dire “Non è vero che tutti i programmi TV sono inguardabili” è lo stesso che dire “C'è almeno un programma TV che non è inguardabile”.
Nell'universo X ={a,b,c,d,…} l'applicazione del quantificatore esistenziale alla funzione logica p(x) afferma che la p(x) è vera per almeno un elemento di X, cioè che è vera la disgiunzione logica
![]()
La negazione di questa disgiunzione, per le prime leggi di De Morgan, equivale alla congiunzione delle negazioni
![]()
cioè: sono vere tutte le negazioni.
![]()
Esempio:
Dire “Non è vero che c'è almeno un tipo di sigarette che fa bene” è lo stesso che dire “Tutti i tipi di sigarette non fanno bene”.
L'uso delle seconde leggi di De Morgan può aiutare a comprendere meglio il senso logico dell'implicazione materiale
![]()
e dell'implicazione logica
![]()
Si ha infatti
![]()
traducendo l'ultima proposizione: “Non esiste nessuna x che verifichi p(x) ma non q(x)”, cioè “Tutte le x che verificano p(x) verificano anche q(x)”. In termini insiemistici : “L'insieme di verità di p(x) è incluso nell'insieme di verità di q(x)”.
L'esigenza di un'analisi razionale delle questioni umane (scientifiche e morali) produsse nella Grecia del VI-V secolo a.C. la nascita della filosofia. Un'analisi razionale non può però prescindere dalla definizione di corrette procedure di deduzione per evitare che nei ragionamenti, pur partendo da giuste premesse, si giunga a conclusioni errate o insensate.
Nel più generale ambito della ricerca filosofica si sviluppò ben presto una ricerca specifica sulle corrette modalità di ragionamento. Questa ricerca fu condotta in modo sistematico soprattutto da Aristotele in un complesso di opere in seguito collettivamente indicate con il nome di “Organon”. Anche il vocabolo “Logica” è successivo ad Aristotele (sembra sia dovuto ad Alessandro d'Afrodisia, un suo commentatore del 200 d.C.).
Nelle opere dell'Organon Aristotele analizza i “giudizi”, cioè sostanzialmente le frasi che qui sono state chiamate funzioni logiche, e come da particolari schemi di connessione di diversi giudizi si possa ricavare una sintesi che produce nuova conoscenza. Tali schemi logici furono detti figure di sillogismo.
I sillogismi consistono in una congiunzione di due proposizioni (premessa maggiore e minore) aventi un termine in comune (termine medio) e da un conclusione che correla gli altri due termini. L'importanza dell'analisi aristotelica sta nella affermazione che la validità della conclusione non dipende da ciò di cui si parla, ma dalla forma del sillogismo.
Prima figura.
Il termine medio è soggetto della premessa maggiore, che è un affermazione universale, e predicato della premessa minore, che è un'affermazione particolare, “ Gli uomini sono mortali” e “Socrate è un uomo”. Come conclusione si ha un'affermazione particolare formata attribuendo al soggetto della premessa minore (Socrate) il predicato della premessa maggiore (mortale): “Socrate è mortale”.
Seconda figura.
Il termine medio è predicato in entrambe le premesse e la prima premessa è una negazione universale, la seconda un'affermazione universale: “I mammiferi non hanno penne”, “I merli hanno penne”. Come conclusione si ha una negazione universale formata attribuendo come predicato al soggetto della premessa minore (merli) il del soggetto della premessa maggiore (mammiferi): “I merli non sono mammiferi”.
Terza figura.
Il termine medio è soggetto nelle due premesse, costituite entrambe da affermazioni universali: “I pipistrelli sono mammiferi”, “I pipistrelli volano”. Come conclusione si ha una quantificazione esistenziale sui due predicati: “Qualche mammifero vola”.
Può essere un esercizio stimolante tradurre queste figure di sillogismo nel formalismo logico adottato nei paragrafi precedenti.
Sicuramente la scienza che meglio si prestava ad essere organizzata negli schemi deduttivi aristotelici era la matematica o meglio il ramo della matematica più approfondito dai greci cioè la geometria. (In epoca classica, i greci non svilupparono molto aritmetica e algebra anche a causa di un sistema di notazione numerica complicato e impreciso).
Il frutto finale di questo lavoro furono gli “Elementi” di Euclide, in cui confluirono anche i risultati conseguiti da molti altri matematici precedenti.
Gli “Elementi”, nella storia della cultura occidentale e non solo (si pensi alla cultura araba), furono importantissimi non solo per i matematici ma per tutti gli studiosi intenzionati ad organizzare i risultati delle loro ricerche in schemi chiari e inconfutabili come quelli proposti da Euclide. Così come la Logica era stata un modello per la Geometria, la Geometria diventò un modello per la Logica ma in generale per qualunque scienza.
Ciò fu particolarmente vero per personaggi come W. G. Leibniz (sec. XVIII, contemporaneo di I. Newton) che oltre ad essere importante filosofo fu importante matematico e fisico. Il suo ideale, per risolvere le dispute politiche e morali che dividevano i suoi contemporanei, era di arrivare a matematizzare le questioni filosofiche in modo da giungere a risultati universali e inconfutabili come quelli ottenuti dalla Matematica.
Il programma di Leibniz fu ripreso e largamente attuato per la Logica, nel secolo successivo, dai britannici A. De Morgan, cui si deve la formulazione delle leggi precedentemente ricordate, G. Boole, che per primo propose il formalismo oggi universalmente adottato di calcolo logico e largamente applicato allo hardware e al software dei computer, e J. Venn, che nel calcolo logico usò ampiamente i diagrammi che oggi ne portano il nome.
Nel XX secolo l'opera di B. Russel fa in un certo senso un percorso inverso a quello di Boole: dopo che questi ha matematizzato la Logica, Russel, si impegnò nella logicizzazione dell'Aritmetica e dell'Algebra come unica via per fondarle e svilupparle in modo esente da contraddizioni. La sua influenza sui pensatori del secolo fu talmente ampia che tutto un gruppo di filosofi, denominato “Circolo di Vienna” (R. Carnap, O. Neurath e altri) lavorò intensamente alla logicizzazione di interi campi tradizionalmente appartenenti alla speculazione scientifica o filosofica.
ultima revisione: Settembre 2018