(a cura di Roberto Bigoni)
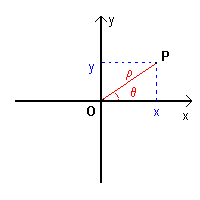
Ogni punto P di un piano su cui è definito un sistema di riferimento cartesiano ortogonale monometrico xOy può essere messo in corrispondenza biunivoca con una coppia ordinata di numeri reali, che sono detti coordinate del punto.
Ciò può essere fatto in due modi fondamentali:

Tra coordinate rettangolari e coordinate polari sussistono le seguenti relazioni
![]()
Viceversa si ha
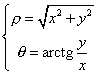
Poiché la funzione tangente è biunivoca solo nell'intervallo
![]() ,
la relazione che esprime θ in funzione delle coordinate rettangolari x e y
è immediatamente valida solo nel primo e quarto quadrante. Se un punto è nel secondo o terzo quadrante,
per ottenere θ, l'arcotangente va aumentata di π.
,
la relazione che esprime θ in funzione delle coordinate rettangolari x e y
è immediatamente valida solo nel primo e quarto quadrante. Se un punto è nel secondo o terzo quadrante,
per ottenere θ, l'arcotangente va aumentata di π.
La seguente applicazione Javascript traduce le coordinate da rettangolari a polari.
Ovviamente funziona solo se il vostro browser consente l'esecuzione di script.
Se il vostro browser non ammette frames interni, potete accedere direttamente alla pagina dell'applicazione.
Data la biunivocità della relazione tra punti piani e coppie di reali, nel seguito dell'esposizione la parola 'punto piano' (o semplicemente 'punto') sarà usata come sinonimo di 'coppia di reali', facendo astrazione dal suo immediato significato geometrico.
Date le coordinate rettangolari di due punti
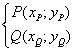
è possibile individuare univocamente un terzo punto
![]()
È legittimo dire che S è la somma di P e Q poiché la relazione tra la coppia (P;Q) e S gode di tutte le proprietà formali della somma di reali.
Infatti essa è interna, associativa, commutativa, ammette un elemento neutro e ogni elemento è invertibile.
L'insieme dei punti piani strutturato con l'operazione di somma è un gruppo.
Inoltre, come la somma di reali, anche la somma di punti è commutativa.
In questo gruppo l'elemento neutro additivo Z, cioè l'elemento che, sommato a qualunque altro elemento P, dà P è, in coordinate rettangolari, Z(0;0). Il modulo di Z è 0, la sua fase è indeterminata.
L'opposto di P(x;y), cioè il punto che sommato a P dà Z è -P(-x;-y).
Un multiplo naturale di ordine n di un punto P è la somma di n punti uguali a P è può essere pensato come il prodotto di n per P, cioè il punto che si ottiene moltiplicando ognuna delle sue coordinate rettangolari di P per n.
Generalizzando, il prodotto di un reale α per un punto P è il punto αP, ottenuto moltiplicando ognuna delle coordinate rettangolari di P per il reale α
![]()
Volendo definire un prodotto interno dei punti P e Q, i due tipi di prodotto definiti nell'algebra dei vettori piani non risultano adeguati:
Un prodotto interno che mantenga tutte le proprietà formali del prodotto sui reali può essere definito in modo abbastanza naturale riferendosi alle coordinate polari, cioè facendo corrispondere ad ogni coppia di punti
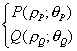
il punto
![]()
cioè il punto T il cui modulo è il prodotto dei moduli e la cui fase è la somma della fasi in modulo 2π
Le proprietà di gruppo di questo prodotto derivano immediatamente da quelle del prodotto di reali.
L'elemento neutro U, in coordinate rettangolari o in coordinate polari, è U(1;0).
Usando il linguaggio dell'algebra vettoriale, U è il versore dell'asse delle ascisse.
Il reciproco di P(ρ ; θ), cioè l'elemento che moltiplicato per P dà l'elemento neutro U, ha coordinate polari
![]()
Ovviamente l'elemento Z, di modulo nullo, non ha reciproco.
Il prodotto di Z per qualunque P produce un elemento di modulo nullo, cioè Z stesso.
Z è l'elemento assorbente del prodotto.
L'insieme dei punti piani C, dotato delle operazioni di somma e prodotto sopra definite, forma la struttura algebrica C(+;∗) nella quale le operazioni di somma e prodotto godono di tutte le proprietà di cui godono in R la somma e il prodotto algebrico.
Inoltre, come in R, la moltiplicazione è distributiva rispetto all'addizione e quindi la struttura C (+;∗) è un campo.
Questo campo, per ragioni storiche, è detto campo dei numeri complessi e i suoi elementi vengono detti numeri complessi.
In questa esposizione si chiameranno complessi rettangolari i numeri complessi espressi in coordinate rettangolari e complessi polari i numeri complessi espressi in coordinate polari.
Se si rappresentano con i simboli u e i i numeri complessi rettangolari u(1;0) e i(0;1), cioè, usando il linguaggio dell'algebra vettoriale, i versori degli assi, tutti i numeri complessi, come i vettori piani, possono essere espressi da combinazioni lineari di u e i.
![]()
Usualmente il versore u viene sottinteso, mentre il versore i, detto unità immaginaria, viene espresso esplicitamente. Quindi un numero complesso z viene di norma rappresentato nel seguente modo, detto forma algebrica dei numeri complessi
![]()
Usualmente, in elettrotecnica, l'unità immaginaria viene rappresentata con il simbolo j, dato che i rappresenta solitamente l'intensità della corrente elettrica.
Le componenti cartesiane rettangolari x e y dei numeri complessi vengono dette rispettivamente parte reale e parte immaginaria.
Quando le parti reale o immaginaria sono nulle, per semplicità di scrittura, solitamente sono omesse.
Ad esempio, l'elemento neutro additivo si scrive 0 e l'elemento neutro moltiplicativo si scrive 1.
Ma bisogna evitare di confonderli con gli analoghi elementi del campo dei reali.
L'insieme dei complessi che hanno parte immaginaria nulla, rappresentati nel piano cartesiano, è l'asse delle x che, in questo contesto, viene detto asse reale.
L'insieme dei complessi che hanno parte reale nulla, rappresentati nel piano cartesiano, è l'asse delle y che, in questo contesto, viene detto asse immaginario.
I punti dell'asse immaginario sono multipli di i e sono espressi quindi da y i.
Il piano, strutturato con un asse reale e un asse immaginario, nel quale si possono rappresentare i numeri complessi in forma algebrica, è detto piano di Gauss (o anche piano di Argand-Gauss).
L'espressione polare dell'unità immaginaria i è
![]()
Il quadrato di i è (1;π), cioè, in coordinate rettangolari, (-1; 0).
Quindi si può scrivere
![]()
La forma algebrica di un numero complesso polare z(ρ ; θ) può essere espressa come
![]()
Questa espressione è detta forma trigonometrica dei numeri complessi.
È inoltre possibile dimostrare che
![]()
e quindi esprimere un complesso z anche nel seguente modo
![]()
Questa espressione è detta forma esponenziale dei numeri complessi.
Se non si ha familiarità con gli sviluppi in serie delle funzioni, una giustificazione intuitiva dell'espressione esponenziale dei numeri complessi può essere ottenuta nel seguente modo.
L'esponenziale naturale con argomento reale x, cioè ex, può essere definita come
![]()
Estendendo questa definizione anche a variabili complesse ix si ha
![]()
Sommando e sottraendo membro a membro queste due uguaglianze si ottiene
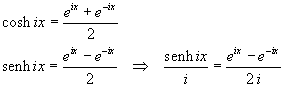
Sommando il quadrato di cosh ix con il quadrato di (senh ix)/i si ha
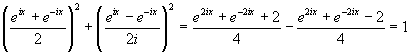
Visto che la somma dei quadrati di queste due funzioni è 1 e che
![]()
esse possano essere identificate con i coseno e il seno di x.
![]()
Si ha allora
![]()
Le identità
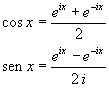
sono note come formule di Eulero per seno e coseno circolari.
Usualmente i numeri complessi sono, come i reali, indicati con lettere latine minuscole. Così come una generica variabile reale viene indicata con x, una generica variabile complessa è indicata con z.
Usualmente inoltre i numeri complessi, a seconda del contesto, vengono scritti o in forma algebrica, facendo riferimento alle loro coordinate rettangolari, o in forma trigonometrica e meglio ancora in forma esponenziale, facendo riferimento alle loro coordinate polari.
Esempio:
Il numero complesso rettangolare z(1;1) in forma algebrica viene scritto 1+i.
Per determinare il reciproco di z conviene esprimere z in forma trigonometrica
![]()
Il reciproco di z in forma trigonometrica è
![]()
![]()
Il reciproco di z in forma esponenziale è
![]()
Il reciproco in forma algebrica è
![]()
È possibile determinare direttamente anche il reciproco della forma algebrica.
Infatti per ogni numero complesso z=x+iy può essere biunivocamente definito il numero
![]()
cioè il complesso che si ottiene da z cambiando il segno della sua parte immaginaria. Questo numero è detto coniugato di z.
Il prodotto di un numero complesso per il suo coniugato coincide con ρ2, cioè con il quadrato del modulo del numero complesso:
![]()
Il quadrato del modulo di z è detto norma di z.
Per ottenere direttamente in coordinate rettangolari il reciproco del complesso rettangolare z sarà sufficiente osservare che
![]()
Il reciproco di un numero complesso è uguale al rapporto tra il suo coniugato e la sua norma.
Dati i due numeri complessi
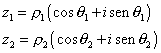
la loro differenza risulta
![]()
La norma ρd2 della differenza è
![]()
![]()
![]()
![]()
Questa identità esprime il teorema di Carnot.
Come in tutti i campi algebrici commutativi anche nel campo dei complessi
La sottrazione è immediata se i numeri sono in forma algebrica, mentre la divisione è immediata se i numeri sono in forma trigonometrica ma rimane abbastanza agevole anche in forma algebrica.
Se il numero complesso è in forma trigonometrica, la potenza con esponente naturale n si deduce immediatamente come prodotto di n fattori uguali.
Dato
![]()
si ha
![]()
Usando la forma esponenziale si ha più direttamente
![]()
Se il numero complesso è noto in forma algebrica, le potenze ad esponente intero intero possono essere ottenute utilizzando il teorema binomiale.
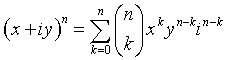
Viceversa, una radice ennesima di z è
![]()
La radice così ottenuta è la radice principale.
Va però osservato che, per la periodicità di seno e coseno, qualunque fase
![]()
genera una radice, in quanto moltiplicando per n tali valori si ottengono argomenti che producono uguali valori per il seno e il coseno.
In definitiva
![]()
o, in forma esponenziale,
![]()
Capita di sentir dire che i è la radice quadrata di -1. Questa affermazione è scorretta se -1 è un numero reale. In campo reale non ci sono quadrati negativi, quindi non ci sono radici quadrate di numeri negativi. Ma non è pienamente corretta nemmeno se -1 è un numero complesso, perché i numeri complessi hanno sempre due radici quadrate. Le radici quadrate del numero complesso -1 sono +i e -i.
Un errore decisamente peggiore è dire che nel campo complesso si possono estrarre radici quadrate di numeri negativi: i numeri complessi non possono essere classificati come positivi o negativi, perché l'insieme dei complessi non è ordinato.
Le due radici quadrate di un numero complesso z = a + ib con a e b diversi da 0 possono essere calcolate direttamente da a e b nel seguente modo.
Se x + iy è la radice cercata, si ha ![]()
![]()
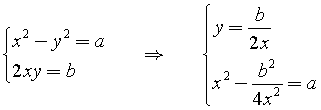
Risolvendo l'equazione in x per valori reali si ottiene
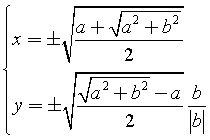
Ad esempio, le radici quadrata di 3+4i sono ±(2+i).
Come nel campo reale, le due radici quadrate sono opposte.
Se si esprime la base in forma esponenziale e l'esponente in forma algebrica, una potenza p di base complessa
![]() ed esponente complesso
ed esponente complesso ![]() è denotata come
è denotata come
![]() .
.
Applicando le note proprietà delle potenze si ottiene
![]()
I fattori
![]() sono evidentemente reali, mentre il fattore
sono evidentemente reali, mentre il fattore
![]() è evidentemente un complesso di modulo 1. Per comprendere la natura del fattore
è evidentemente un complesso di modulo 1. Per comprendere la natura del fattore
![]() si può osservare che ogni potenza di base reale rx può essere trascritta
come
si può osservare che ogni potenza di base reale rx può essere trascritta
come ![]() e quindi
e quindi
![]() .
.
In definitiva
![]()
Esempi:
![]()
Si ha
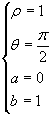
Quindi: 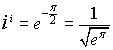
![]()
Si ha
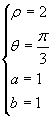
Quindi: 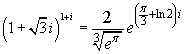
Il logaritmo naturale di un numero complesso è immediato se si scrive il complesso in forma esponenziale.
Da ![]() si ottiene
si ottiene
![]()
Tuttavia, analogamente a quanto si è osservato nel caso dell'estrazione della radice n-esima di un complesso, va osservato che la fase è periodica con periodo 2π e quindi, accanto a quello che può essere considerato il valore di base del logaritmo, vanno ammessi come logaritmi di z anche tutti i numeri
![]()
in cui k può assumere tutti i valori interi relativi.
Ad esempio
Dato il numero complesso z espresso in forma algebrica
![]() ,
estendendo al campo complesso le
formule di addizione per seno e coseno circolari, si ottiene
,
estendendo al campo complesso le
formule di addizione per seno e coseno circolari, si ottiene
![]()
Dalle formule di Eulero si ha inoltre
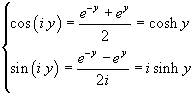
e quindi
![]()
in modo analogo si ottiene
![]()
Per le funzioni iperboliche si ha
![]()
![]()
Dato ![]() , quali sono le radici
quinte di z5?
, quali sono le radici
quinte di z5?
Si ha
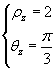
dunque
![]()
da cui
![]()
In dettaglio:
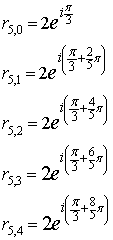
Volendo scrivere questi cinque numeri in notazione algebrica, dal testo del problema si ha ovviamente
![]()
Per calcolare coseno e seno delle anomalie degli altri quattro numeri si possono usare le formule di addizione, ricordando che nei triangoli aurei di primo tipo il rapporto tra base e lato è φ, si ha
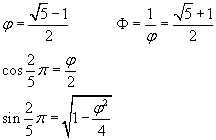
Per l'angolo esplementare si ha
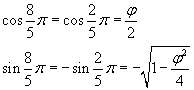
Con le formule di duplicazione si ha
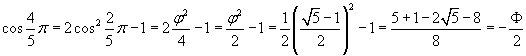
e quindi
![]()
Per l'angolo esplementare si ha
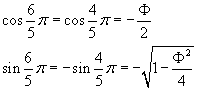
Si possono ora calcolare seni e coseni delle anomalie. Ad esempio
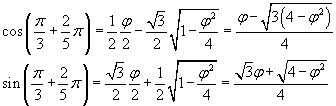
quindi
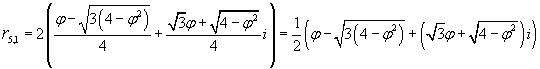
Wolfram|Alpha è un portale che ha l'ambizione di soddisfare ogni nostro desiderio di conoscenza. In particolare rende disponibili in rete alcune potenti funzionalità di Mathematica, il noto software prodotto dalla Wolfram.
Wolfram|Alpha può essere interrogato scrivendo nel suo campo di input frasi in linguaggio naturale (ovviamente inglese) o anche solo una sequenza di parole chiave. Ma dato che nel campo di input ci si scrive con la tastiera, se si intende richiedere l'esecuzione di calcoli matematici, conviene impostarli usando il linguaggio nativo di Mathematica.
Per chi non conoscesse questo linguaggio può essere utile consultare la pagina Mathematica con WolframAlpha di questo sito.
Esempio.
Prodotto di complessi: (2+3I)(1/2-I)
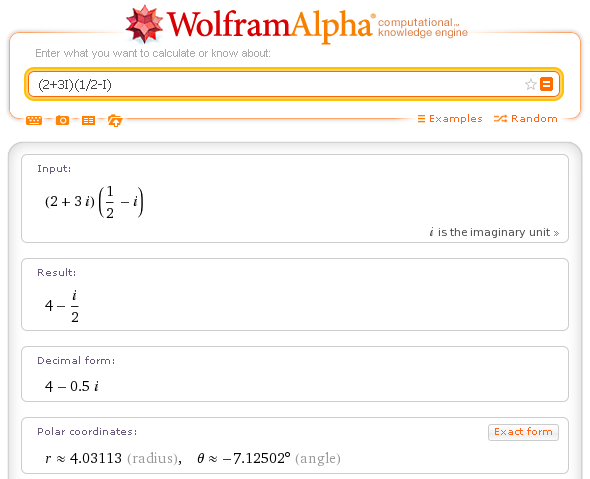
Altri esempi.
Quoziente di complessi: (2+3I)/(1/2-I)
Potenza intera di complesso: (1/2-I)^4
Potenza complessa di intero: 2^I
Potenza complessa di complesso: I^I
Radice quadrata di complesso: Sqrt[1+I Sqrt[3]]
WolframAlpha - Radice quadrata
Seno di complesso: Sin[I]
In questo sito è disponibile l'applicazione SuperCalcolatrice che permette il calcolo numerico anche sul campo dei numeri complessi.
Può essere interessante la rappresentazione di un particolare insieme di numeri complessi: l'Insieme di Mandelbrot.
ultimo aggiornamento: 18/03/2018