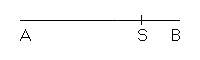
In modo analogo a quello seguito nella sezione aurea di un segmento si può effettuare la sezione plastica di un segmento AB individuando il suo punto S tale che il cubo di spigolo AS sia equivalente al parallelepipedo rettangolo di spigoli AB, SB e AB+AS.
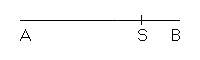
![]()
Questa definizione è dovuta all'architetto-monaco benedettino Hans Van der Laan(1904-1991) che l'applicò al progetto di edifici religiosi.
Indicando con λ la misura del segmento AB e con σ la misura del segmento AS si ha
![]()
equivalente a
![]()
Indicando con x il rapporto tra λ e σ si ha
![]()
Se si rappresentano nell stesso piano cartesiano le curve di equazione y=x3 e y=x+1 si osserva che esse si intersecano in un unico punto di ascissa compresa tra 1 e 2: dunque l'equazione ammette un'unica soluzione reale.
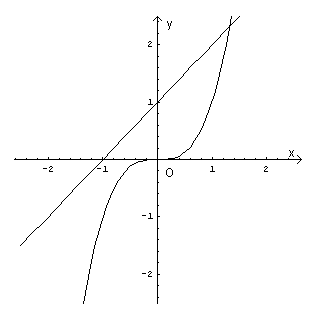
La soluzione reale dell'equazione è detta numero plastico (o costante plastica) e, in questa sede, tale numero viene denotato con P. L'equazione viene detta "equazione plastica".
Per calcolare P si può risolvere l'equazione plastica con il metodo di Cardano procedendo nel seguente modo
Si riscrive l'equazione nella variabile w
![]()
Si ottiene
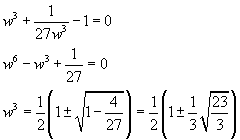
Le radici reali dell'equazione in w sono dunque
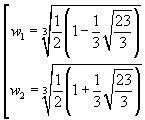
Per semplicità si omettono le radici complesse. Sostituendo l'uno o l'altro dei due valori w1 e w2 nell'espressione di x con una calcolatrice si ottiene una approssimazione alla soluzione P dell'equazione:
P≈1.3247179572447460...