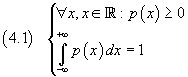
Se una variabile casuale reale x può assumere qualunque valore reale, una funzione reale continua p(x) tale che
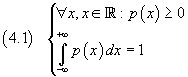
è detta funzione di densità di probabilità.
La probabilità dell'evento [a,b] è data da
Generalizzando le definizioni di media e varianza date nella sezione precedente per le distribuzioni discrete
il valor medio di x è dato da
la media del quadrato degli scarti è
quindi la varianza è
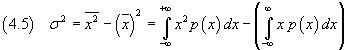
Esempio.
Se p(x) è espressa da
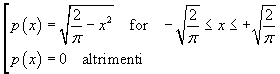
p(x) è una densità di probabilità. Infatti, nell'intervallo in cui è maggiore di 0, è graficamente rappresentata
da una semicirconferenza di raggio
. L'area del semicerchio e quindi
l'integrale da -∞ a +∞, è 1.
Una funzione p(x) tale che
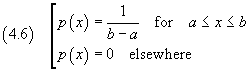
è detta distribuzione continua uniforme
Il valor medio è
La media dei quadrati è
La varianza è
e la deviazione standard
Dato un valore reale positivo λ(lambda), una funzione p(x) tale che
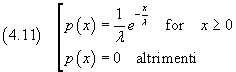
è detta distribuzione continua esponenziale.
Questa funzione è sempre > 0 e
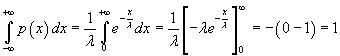
Il valor medio è
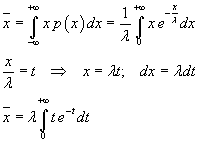
Integrando per parti
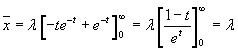
Il valor medio dei quadrati è
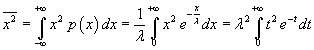
Integrando per parti
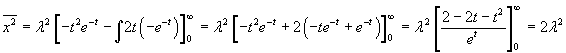
La varianza è
e la deviazione standard
La seguente applicazione JS rappresenta una distribuzione esponenziale di λ prefissato.
Per visualizzare le tabelle bisogna che il browser in uso consenta i popup.
La seguente applicazione JS permette di calcolare la probabilità che in una distribuzione esponenziale di λ prefissato un evento assuma valori compresi tra x1 e x2
Dati due numeri reali positivi A e a, una funzione p(x) tale che
è una funzione di densità di probabilità se
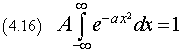
Dato che p(x) è una funzione pari, questa uguaglianza è equivalente alla seguente
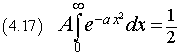
Si può dimostrare che
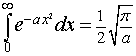
quindi
In definitiva p(x) dipende solo dal parametro a
Dato che p(x) è una funzione pari, il suo valor medio è 0 e la sua varianza è
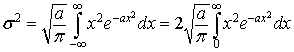
Si dimostra che
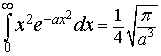
quindi
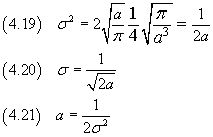
Conviene scrivere p(x) direttamente in funzione della sua varianza
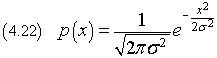
La funzione(4.22) è detta distribuzione gaussiana. Il suo grafico è la nota curva a campana, simmetrica rispetto all'asse delle ordinate, con un massimo per x=0 e flessi per x=±σ.
Se si trasla la curva di una quantità μ, la sua equazione è espressa da
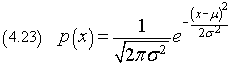
La seguente applicazione JS rappresenta una distribuzione gaussiana di σ prefissato.
Per visualizzare le tabelle bisogna che il browser in uso consenta i popup.
La seguente applicazione JS permette di calcolare la probabilità che in una distribuzione gaussiana con media 0 e σ prefissato un evento assuma valori compresi tra x1 e x2