(a cura di Roberto Bigoni)
Una circonferenza ottenuta intersecando una superficie sferica di raggio R con un piano passante per il suo centro, cioè una delle circonferenze di raggio massimo ottenibili sulla superficie sferica, è detta geodetica. Il piano secante è il generatore della geodetica.
Ad esempio, supponendo che la Terra sia una sfera perfetta, i meridiani sono geodetiche, ma tra i paralleli, l'unica geodetica è l'equatore.

Due geodetiche diverse si intersecano in due punti diametralmemte opposti P e Q.
I loro piani generatori formano due coppie di diedri opposti al vertice. Ogni diedro di misura λ individua sulla superficie sferica una regione delimitata da due semicirconferenze di estremi P e Q detta luna di vertici P e Q e lati PAQ e PBQ. I punti P e Q sono i vertici di due angoli sferici entrambi di misura λ. Si dirà anche che la luna PAQB è una luna Λ di angolo λ.
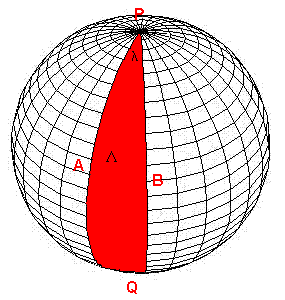
L'area l di una luna Λ di angolo λ sta alla superficie della sfera come l'angolo λ sta a 2π.
![]()
quindi
![]()
L'insieme di tutte le geodetiche che si intersecano negli stessi punti P e Q è detto fascio di geodetiche di poli PQ.
Ad esempio, due meridiani terrestri si intersecano nei poli N e S.
L'insieme di tutti i meridiani è un fascio di geodetiche di poli NS.
Intersecando una luna Λα di angolo α di un fascio di poli AZ con una terza geodetica che non appartenga allo stesso fascio e che quindi intersechi i lati di Λα nei punti B e C, si divide la luna Λα in due regioni di vertici ABC e ZBC dette triangoli sferici.
L'area del triangolo ZBC si ottiene sottraendo dall'area della luna Λα l'area del triangolo ABC.
![]()
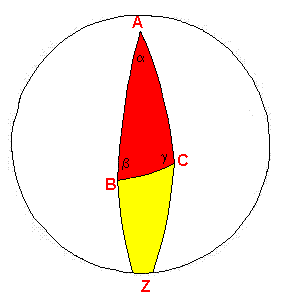
Il triangolo ABC è dato dall'intersezione delle lune Λβ di angolo β e Λγ di angolo γ. Dunque l'area dell'unione di Λβ e Λγ è data dalla somma delle loro singole aree diminuita dell'area del triangolo ABC (che, altrimenti, verrebbe valutato due volte).
![]()
Se all'unione delle lune Λβ e Λγ si unisce poi il triangolo individuato dagli antipodi di Z, B e C, congruente con il triangolo ZBC, si copre una semisfera. Dunque sommando all'area dell'unione di Λβ e Λγ, l'area del triangolo ZBC si ottiene l'area della superficie della semisfera.
![]()
Unendo questi risultati si ottiene
![]()
e quindi l'area del triangolo sferico:
![]()
Dato che l'area di un triangolo sferico deve essere positiva, si deduce che la somma degli angoli interni di un triangolo sferico è maggiore di un angolo piatto.
Questo risultato è evidente nel fascio dei meridiani terrestri: due meridiani distinti formano entrambi angoli retti con l'equatore e, convergendo in un polo, formano un angolo dato dal valore assoluto della differenza tra le loro longitudini. Quindi sulla superficie terrestre in un triangolo sferico, delimitato da due meridiani distinti e dall'arco di equatore tra di essi, la somma degli angoli interni è maggiore di due angoli retti.
Si consideri un poliedro Π a facce triangolari e sia F il numero delle sue facce, V il numero dei suoi vertici e S il numero di suoi spigoli. Si consideri quindi una superficie sferica Σ di raggio R contenente il poliedro e da un punto interno a Π si proiettino gli spigoli di Π stesso su Σ. Ad ognuna delle facce di Π corrisponderà un triangolo sferico, ad ognuno degli spigoli di Π corrisponderà un lato di un triangolo e ad ogni vertice di Π corrisponderà un punto in cui convergono i lati dei triangoli contigui.
L'area di ogni triangolo sferico è data dal prodotto della differenza tra la somma dei suoi angoli interni e l'angolo piatto per il quadrato del raggio. L'area della superficie sferica è uguale alla somme delle aree, cioè alla somma di tutti gli angoli dei triangoli meno tanti angoli piatti quante sono le facce. La somma di tutti gli angoli interni è tanti angoli giro quanti sono i vertici. Quindi
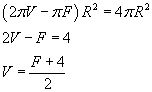
Il numero dei lati S è uguale alla metà del triplo del numero della facce, perché ogni lato è comune a due triangoli contigui:
![]()
Allora
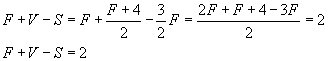
Se Π ha facce poligonali (quindi non necessariamente triangolari) la sua proiezione su Σ sarebbe
un reticolato di poligoni sferici che, nel caso avessero più di tre lati, potrebbero essere suddivisi in triangoli
tracciando le loro diagonali. Per ogni diagonale tracciata, si ha un incremento di un'unità sia nel numero dei
lati sia nel numero delle facce e la relazione tra i numeri di facce, spigoli e vertici rimane immutata.
Dunque in generale si ha che
in ogni poliedro la somma del numero delle facce e dei vertici supera di due unità
il numero degli spigoli.
Questo risultato è uno dei più noti e notevoli tra quelli ottenuti da Eulero.
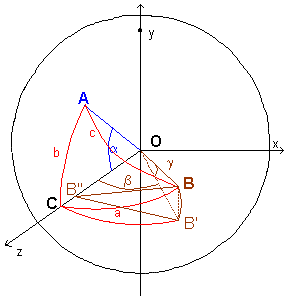
Su una superficie sferica Σ di raggio R e centro O, si consideri un triangolo sferico di vertici A, B e C tale che l'angolo interno ACB sia retto. Si indicano con a, b e c le misure dei lati opposti rispettivamente ad A, B e C.
In questo caso è possibile determinare un sistema di riferimento cartesiano ortogonale con origine nel centro O tale che il piano Oyz coincida con il piano generatore del lato AC e il piano Oxz coincida con il piano generatore del lato BC.
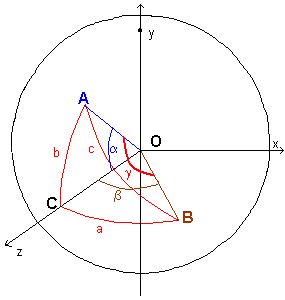
I segmenti OA, OB possono essere descritti come vettori di modulo R. Indicando con α la misura dell'angolo AOC, con β la misura dell'angolo BOC, e con i, j e k i versori degli assi si ha:
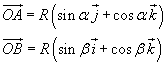
Il prodotto scalare dei due vettori risulta
![]()
Il prodotto scalare dei due vettori può essere ottenuto anche dal prodotto dei loro moduli per il coseno dell'angolo AOB di misura γ:
![]()
Si ottiene quindi
![]()
e, poiché la misura in radianti di un angolo al centro di una circonferenza si ottiene dal rapporto tra arco e raggio,
![]()
Il risultato ottenuto rappresenta una generalizzazione del teorema di Pitagora. Infatti da
![]()
si ottiene
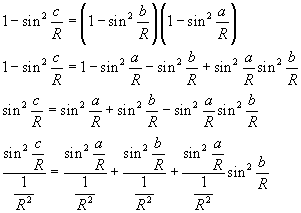
Se si aumenta il raggio della superficie sferica all'infinito, in modo tale che su di essa una regione limitata
diventi indistinguibile da una regione piana, si deve calcolare il limite di questa identità per
![]() . Si ottiene:
. Si ottiene:
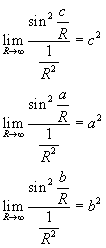
ma
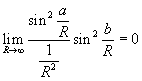
Quindi al limite si ha
![]()
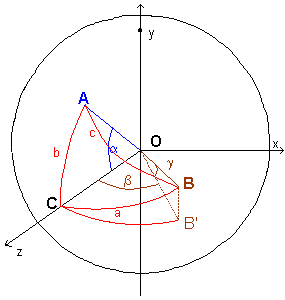
Siano A e B due punti su una superficie sferica di raggio R. Indicando con C il punto dell'equatore sullo stesso meridiano di A e assumendo il meridiano di A come meridiano zero, i vettori OA e OB in coordinate cartesiane sono espressi da
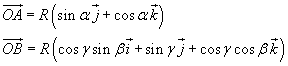
Il prodotto scalare dei due vettori è
![]()
Il prodotto scalare è dato anche da
![]()
quindi
![]()
La distanza AB, sulla superficie sferica, si ottiene quindi da
![]()
In particolare, assumendo la Terra sferica, se A e B sono due luoghi della superficie terrestre, si ha
![]()
Esempio: calcolo della distanza (in linea d'aria) tra New York e Cape Town.
| luogo | latitudine | longitudine |
|---|---|---|
| New York | 40°45'25"N | 73°59'10"W |
| Cape Town | 33°54'58"S | 18°25'19"E |
Si decimalizzano le misure angolari.
| luogo | latitudine | longitudine |
|---|---|---|
| New York | 40.757140° | -73.986053° |
| Cape Town | -33.916156° | 18.422012° |
Si esprimono le misure angolari in radianti (necessario se si usa un foglio elettronico o un linguaggio di programmazione).
| luogo | latitudine | longitudine |
|---|---|---|
| New York | 0.711346 | -1.291300 |
| Cape Town | -0.591949 | 0.321525 |
Si calcola la differenza di longitudine:
![]()
Si calcola l'angolo γ:
![]()
Infine la distanza si ottiene moltiplicando γ per il raggio medio della Terra:
![]()
Misure ottenute con calcoli più elaborati,
basati sul fatto che la Terra non è una sfera perfetta ma un elissoide,
dànno una distanza di 12552km.
Come si vede l'errore è dell'ordine dell'1‰.
La seguente applicazione Javascript calcola la lunghezza di un arco sferico date le coordinate angolari, cioè latitudine e longitudine, degli estremi A e B (evitare punti diametralmente opposti). Le coordinate angolari possono essere scritte in gradi sessagesimali ggg°pp'ss" (è necessario almeno uno dei tre separatori) o in radianti (decimale puro). Se non è presente almeno un separatore sessagesimale la misura si intende in radianti. È possibile usare la costante P per rappresentare π.
Se il browser in uso non ammette il tag iframe potete visualizzare direttamente la pagina dell'applicazione.
Se i punti A e B sono su una superficie sferica di raggio unitario, si ha

Si ha inoltre
![]()
Sostituendo i secondi membri di queste identità nell'equazione
![]()
si ottiene
![]()
Questa identità esprime una relazione tra un lato (c) e gli altri due (a e b) in funzione del coseno dell'angolo formato da questi due. Rappresenta quindi la versione sferica del noto teorema del coseno della trigonometria piana. Se l'angolo ACB è retto si ottiene il teorema di Pitagora.
Dalle misure dei lati si possono quindi ricavare i coseni degli angoli interni del triangolo:
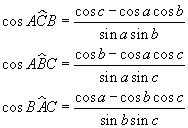
Per una sfera di raggio R si ha
![]()
e quindi
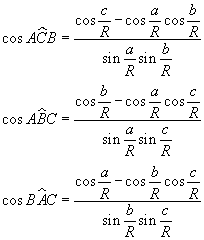

Dato il triangolo sferico di vertici A, B e C su una superficie sferica Σ di raggio unitario
e centro O, noti gli angoli α, β e γ della figura (cioè latitudini e longitudini
di A, B e C rispetto ad un qualunque sistema di riferimento di Σ),
dette a, b e c le misure dei lati,
le misure degli angoli interni
![]() possono essere dedotte
dalle misure di a, b e c usando il teorema del coseno. L'area del triangolo, come s'è
visto nel paragrafo 2, si ottiene sottraendo π dalla somma degli angoli interni. La misura di quest'area
coincide con la misura in steradianti dell'angolo solido con vertice in O e lati determinati dalle intersezioni
dei semipiani generatori dei lati del triangolo.
possono essere dedotte
dalle misure di a, b e c usando il teorema del coseno. L'area del triangolo, come s'è
visto nel paragrafo 2, si ottiene sottraendo π dalla somma degli angoli interni. La misura di quest'area
coincide con la misura in steradianti dell'angolo solido con vertice in O e lati determinati dalle intersezioni
dei semipiani generatori dei lati del triangolo.
Se Σ ha raggio R, gli steradianti vanno moltiplicati per R2.
Conviene implementare questa procedura in un foglio elettronico o in un linguaggio di programmazione sequenziale. Qui si presenta una versione in Javascript. Latitudini e longitudini possono essere scritte in gradi sessagesimali ggg°pp'ss" (è necessario almeno uno dei tre separatori) o in radianti (decimale puro). Evitare punti diametralmente opposti. È possibile usare la costante P per rappresentare π.
Se il browser in uso non ammette il tag iframe potete visualizzare direttamente la pagina dell'applicazione.
A, B e C sono tre punti su una superficie sferica di centro O e raggio R.
Si traccino i raggi dal centro ai vertici e si indichino con α, β e γ gli angoli da essi formati. Si consideri il piano per C perpendicolare al piano dei raggi OA e OB e siano A' e B' le intersezioni di questo piano con i due raggi. Si consideri il triangolo CA'B' e sia CH l'altezza, di misura h, di questo triangolo rispetto al lato A'B'.
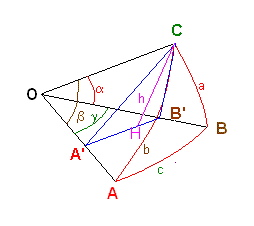
Applicando note relazioni di trigonometria piana, si ottiene
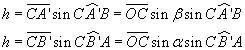
e quindi
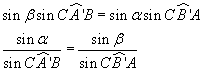
Gli angoli nei denominatori coincidono con gli angoli nei vertici del triangolo sferico, mentre quelli nei numeratori sono dati dai rapporti tra i lati del triangolo sferico e il raggio. Dunque
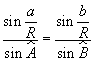
La stessa costruzione può essere ripetuta tracciando il piano perpendicolare per uno degli altri due vertici, quindi in generale
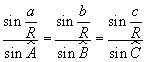
Per ![]() , la relazione
ottenuta converge al teorema dei seni della trigonometria piana.
, la relazione
ottenuta converge al teorema dei seni della trigonometria piana.
ultima revisione: 03/11/2018