Una successione si dice geometrica quando il rapporto q tra ogni elemento e il precedente è costante. Il rapporto costante q è detto ragione geometrica.
Dati il primo elemento a0 e la ragione q, una successione geometrica è immediatamente definita in modo ricorsivo:
![]()
Osservando che
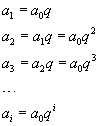
si ottiene agevolmente anche la definizione intensiva della successione.
La somma delle prime n potenze di un numero reale q (q ≠ 0, q ≠ 1)
![]()
può essere agevolmente ottenuta osservando che
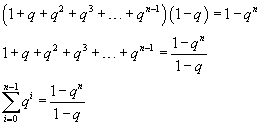
Esempio
La somma delle prime dieci potenze di 2, cioè da 1 a 29 è
![]()
1023 è il massimo numero naturale che può essere codificato in 10 bit.
1023 è il numero di sottinsiemi di un insieme di 10 elementi.
Data una successione geometrica di ragione q e iniziante con a0, la somma dei primi n elementi è
![]()
Sostituendo gli elementi ai con la loro espressione ricorsiva, si ottiene
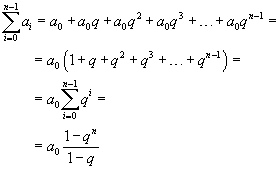
Esempio
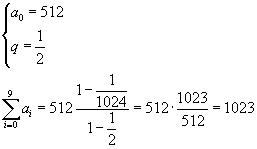
Il confronto tra successioni aritmetiche e geometriche è la base della legge di Malthus
La somma di n elementi in progressione geometrica trova applicazione, ad esempio, nel calcolo delle rate dei mutui a rata costante.