Appunti per i Licei Scientifici
(a cura di Roberto Bigoni)
Chi, disponendo di un capitale finanziario C, lo rende disponibile ad altri per un periodo prefissato, solitamente stipula un contratto che, come remunerazione del servizio, prevede alla scadenza del periodo, oltre alla restituzione del capitale C, il pagamento di un importo aggiuntivo I.
Un contratto di questo genere è detto contratto di mutuo;
chi concede il capitale è detto mutuante; chi lo riceve è detto
mutuatario; il capitale concesso C è detto mutuo;
l'importo aggiuntivo I è detto interesse; la somma di capitale e
interesse
![]() è detta montante.
è detta montante.
L'interesse I solitamente è proporzionale al mutuo C:
![]() .
La costante di proporzionalità i è detta tasso unitario di interesse
relativo al periodo prefissato, detto periodo di capitalizzazione .
.
La costante di proporzionalità i è detta tasso unitario di interesse
relativo al periodo prefissato, detto periodo di capitalizzazione .
Usualmente il tasso di interesse è espresso in percentuale. Per ottenere il tasso unitario il tasso percentuale va diviso per 100.
Al termine di un periodo di capitalizzazione si ha quindi che il montante è espresso da
![]()
Se la durata del mutuo comprende due periodi di capitalizzazione, il montante al termine del secondo periodo dovrà essere calcolato assumendo come capitale iniziale il montante maturato al termine del primo periodo. Si ha quindi
![]()
In generale, per n periodi di capitalizzazione si ha
1) ![]()
Questo metodo di calcolo del montante è noto come regime di capitalizzazione composta.
Il periodo di capitalizzazione cui risulta più conveniente riferirsi è l'anno civile, quindi usualmente si indica con il simbolo i il tasso unitario annuo di capitalizzazione composta. È tuttavia frequente il caso in cui la capitalizzazione avviene con un ritmo più frequente e viene quindi calcolata k volte all'anno:
In generale, se con ik si indica il tasso unitario di interesse relativo al sottomultiplo di ordine k dell'anno, perché una capitalizzazione eseguita k volte in un anno produca lo stesso montante di una capitalizzazione eseguita solo una volta al termine dell'anno, deve essere
![]()
e quindi
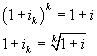
In definitiva
2)
![]()
ik è detto tasso unitario periodico equivalente al tasso annuo unitario i.
Se un contratto di mutuo a capitalizzazione periodica k dura n anni, si ha
3)
![]()
Il mutuante si priva del capitale C per tornare in possesso del montante Mn tra n anni. Volendo, potrebbe oggi scambiare con un terzo il proprio diritto alla riscossione futura di Mn, richiedendo in contraccambio esattamente il capitale mutuato C. In questa prospettiva, si dice che C è il valore attuale di Mn. Dalla 1) si ha
![]()
Cambiando il simbolismo, se con C si indica un capitale disponibile tra n anni e con An il suo valore attuale, si può dire che
4) ![]()
Analogamente, se la capitalizzazione è calcolata k volte all'anno, dalla 3) si ha
5) ![]()
Uno dei più frequenti contratti di mutuo prevede che il mutuatario, invece di restituire al mutuante il montante M al termine della durata del contratto, provveda ad estinguere gradualmente il proprio debito con pagamenti periodici, k volte all'anno, di uguale importo R. Ognuno di questi pagamenti è detto rata di ammortamento e questo metodo di estinzione del mutuo è detto ammortamento a rata costante (o francese).
Il calcolo della rata R si basa sul fatto che la somma dei valori attuali di tutte le rate future, valutati al momento del contratto, deve coincidere con il capitale mutuato C. Deve cioè essere
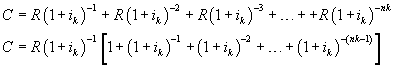
Gli addendi della somma tra parentesi quadre sono nk e sono in
successione geometrica
di ragione
![]() . La loro somma è quindi
. La loro somma è quindi
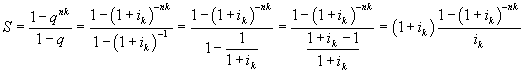
In definitiva si ottiene
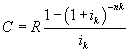
e quindi
6) 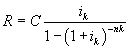
Questa espressione può essere facilmente implementata come funzione in un linguaggio di programmazione. Ad esempio in Javascript
function calcoloRata(m,n,i,k)
{
var m = parseInt(m); //capitale mutuato
var n = parseInt(n); // n. anni
i = parseFloat(i)/100; // dal tasso percentuale a quello unitario
k = parseInt(k); // periodizzazione
var kn = k*n;
var ik = i/k;
var ikpiu1 = ik+1;
var rata = m*ik/(1-Math.pow(ikpiu1,-kn));
return arrotonda(rata);
}
//funzione ausiliaria per l'arrotondamento al centesimo
function arrotonda(x)
{
return Math.round(x*100)/100;
}
Il codice XHTML di una form che interagisca con la funzione può essere il seguente.
<form id="dati" name="dati" style="text-align:center"> <p><label for="mutuo">mutuo</label> <input type="text" name="mutuo" id="mutuo" size="10" value="100000" style="text-align:right"/>€ </p> <p><label for="durata">durata</label> <input type="text" name="durata" id="durata" size="3" value="10" style="text-align:right"/>anni <label for="tasso">tasso</label> <input type="text" name="tasso" id="tasso" size="5" value="5" style="text-align:right"/>% </p> <p> <label for="periodo">periodicità</label> <select id="periodo" name="periodo"> <option value="12">mensile</option> <option value="6">bimestrale</option> <option value="4">trimestrale</option> <option value="3">quadrimestrale</option> <option value="2">semestrale</option> <option value="1">annuale</option> </select> </p> <p> <input type="button" value=" calcolo della rata " onclick="rata.value=calcoloRata(mutuo.value,durata.value,tasso.value,periodo.value)"/> </p> <p><label for="rata">rata</label> <input type="text" name="rata" id="rata" size="12" value="" style="text-align:right"/>€ </p> </form>
Un mutuatario che desideri comparare contratti di mutuo proposti da varie finanziarie, è sicuramente interessato a dedurre, dati l'importo di un mutuo C e l'importo R della rata periodica necessario ad estinguerlo, il tasso effettivo annuo di interesse applicato sull'ammortamento del mutuo stesso.
Un problema analogo si pone quando un mutuatario contrae un mutuo a tasso variabile e, osservando che la finanziaria ha cambiato l'importo della rata periodica, desidera valutare la variazione del tasso di interesse.
In questo caso bisogna risolvere l'equazione 6) rispetto all'incognita ik per poi ricavare dal tasso periodico, tramite la relazione inversa alla 2) il valore del tasso effettivo annuo.
L'equazione 6), posta nella forma equivalente
![]()
appare piuttosto complicata da risolvere analiticamente. Conviene approssimarne la soluzione ad una precisione finanziariamente sufficiente con un metodo numerico, ad esempio con il semplice algoritmo di bisezione.
Il codice Javascript da utilizzare a questo scopo può essere il seguente.
//variabili globali
var rapporto = 0;
var nk = 0;
//implementazione della funzione
function f(x)
{
return (1-rapporto*x)*Math.pow(1+x,nk)-1;
}
//funzione di i/o con la pagina XHTML
function calcoloTasso(mutuo,rata,anni,periodo)
{
var m = parseFloat(mutuo);
var r = parseFloat(rata);
var n = parseInt(anni)
var k = parseInt(periodo);
rapporto = m/r;
var nk = n*k;
if (rapporto>=nk)
{
alert("dati incongruenti");
return undefined;
}
var ik = bisezione(0.00001,1); // algoritmo di bisezione
var ia = Math.pow(1+ik,k)-1; // calcolo del tasso effettivo annuo
ia *=100; // sua espressione in percentuale
return arrotonda(ia); //arrotondamento al centesimo
}
//implementazione ricorsiva dell'algoritmo di bisezione
function bisezione(a,b)
{
var fa = f(a);
if (fa==0) return a;
var fb = f(b);
if (fb==0) return b;
var m = (a+b)/2;
var fm = f(m);
if (fm==0) return m;
if ((b-a)<1e-8) return m;
if (fa*fm<0)
return bisezione(a,m)
else
return bisezione(m,b);
}
La form nella pagina XHTML può essere confezionata così.
<form id="dati1" name="dati1" style="text-align:center"> <p><label for="mutuo1">mutuo</label> <input type="text" name="mutuo1" id="mutuo1" size="10" value="100000" style="text-align:right"/>€ </p> <p><label for="rata">rata</label> <input type="text" name="rata1" id="rata1" size="12" value="1100" style="text-align:right"/>€ </p> <p> <label for="periodo1">periodicità</label> <select id="periodo1" name="periodo1"> <option value="12">mensile</option> <option value="6">bimestrale</option> <option value="4">trimestrale</option> <option value="3">quadrimestrale</option> <option value="2">semestrale</option> <option value="1">annuale</option> </select> </p> <p><label for="durata1">durata</label> <input type="text" name="durata1" id="durata1" size="3" value="10" style="text-align:right"/>anni </p> <p> <input type="button" value=" calcolo del tasso " onclick="tasso1.value=calcoloTasso(mutuo1.value,rata1.value,durata1.value,periodo1.value)"/> <p> <label for="tasso1">tasso</label> <input type="text" name="tasso1" id="tasso1" size="10" value=" " style="text-align:right"/>% </p> </p> </form>
Ognuna delle rate R pagate nell'ammortamento di un mutuo adempie a due funzioni:
Ai fini fiscali è importante conoscere la quota Ik della rata destinata al pagamento degli interessi; questa quota è data dall'interesse che bisognerebbe pagare sul valore del debito Dk-1 all'inizio del periodo di capitalizzazione considerato.
Nella prima rata D0 coincide con C, per cui
![]()
La quota C1 di rimborso del capitale è
![]()
Dopo il pagamento della prima rata il debito residuo D1 è quindi
![]()
L'interesse nel secondo periodo risulta
![]()
la quota di capitale nella seconda rata è
![]()
e il debito rimanente è
![]()
Proseguendo in questo modo è possibile compilare una tabella, detta piano di ammortamento, in ogni riga della quale, in corrispondenza del pagamento di ogni rata, compare la quota interessi, la quota capitale, il debito rimanente e il debito estinto.
Il codice Javascript per calcolare il piano di ammortamento può essere il seguente.
//variabile globale
tabella = "";
function calcoloPiano(m,n,i,k)
{
m = parseInt(m);
n = parseInt(n);
i = parseFloat(i)/100;
k = parseInt(k);
//numero di rate
var kn = k*n;
//interesse periodico equivalente
var ik = i/k;
var ikpiu1 = ik+1
//calcolo della rata costante
var rata = m*ik/(1-Math.pow(ikpiu1,-k*n));
var r = arrotonda(rata); //arrotondamento al centesimo
i=0; //contatore
var Ii = 0; //quota interessi
var Ci = 0; //quota capitale
var Di = m; //debito residuo
var Ei = 0; //debito estinto
//intestazione della tabella
tabella = " k rata q.cap. q.int. d.res. d.est.\n";
var riga = format(0,3,false)+format(0,15,true)+format(Ci,15,true)+format(Ii,15,true)+format(Di,15,true)+format(Ei,15,true)+"\n";
tabella += riga;
//righe successive
for (i=1; i<=kn; i++)
{
Ii = ik*Di;
Ci = rata-Ii;
Di = Di-Ci;
Ei += Ci;
riga = format(i,3,false)+format(r,15,true)+format(Ci,15,true)+format(Ii,15,true)+format(Di,15,true)+format(Ei,15,true)+"\n";
tabella += riga;
}
}
//funzione ausiliaria per normalizzare la rappresentazione dei dati in output
function format(n,campo,decimale)
{
var l = 0;
var s;
if (decimale)
{
n = arrotonda(n);
s = String(n);
l = s.length;
var punto = s.indexOf('.');
if (punto<0) s +='.00';
if (punto==l-1) s +='00';
if (punto==l-2) s +='0';
punto = s.indexOf('.');
s = s.substr(0,punto+3);
}
else
s = String(n);
l = s.length;
while (l<campo)
{
s = " "+s;
l++;
}
return s;
}
La form nella pagina XHTML può essere confezionata così.
<form style="text-align:center"> <p><label for="mutuo">mutuo</label> <input type="text" name="mutuo" id="mutuo" size="10" value="100000" style="text-align:right"/>€ </p> <p><label for="durata">durata</label> <input type="text" name="durata" id="durata" size="3" value="10" style="text-align:right"/>anni <label for="durata">tasso</label> <input type="text" name="tasso" id="tasso" size="5" value="5" style="text-align:right"/>% </p> <p> <label for="periodo">periodicità</label> <select name="periodo"> <option value="12">mensile</option> <option value="6">bimestrale</option> <option value="4">trimestrale</option> <option value="3">quadrimestrale</option> <option value="2">semestrale</option> <option value="1">annuale</option> </select> </p> <p> <input type="button" value=" calcolo " onclick="calcoloPiano(mutuo.value,durata.value,tasso.value,periodo.value); c_piano.value=tabella"/> </p> <p>piano di ammortamento</p> <textarea id="c_piano" rows="10" cols="100" readonly="readonly"> </textarea> </p> </form>
Se gli utenti non sono interessati agli aspetti matematici e informatici, gli stessi risultati possono più direttamente essere ottenuti nella pagina Mutui di questo sito.
ultimo aggiornamento: Ottobre 2016