Serie

6. Serie geometrica

Si dice serie geometrica la somma di tutte le potenze ad esponente naturale (0 incluso) di un numero reale q ≠ 0.

Se q = -1 la serie è indeterminata.
Per q diversi si ha
- Se q ≥ 1, è g diverge positivamente.
- Se q < -1 g diverge negativamente.
- Se -1 < q < +1 (ma ≠ 0), per le proprietà delle successioni geometriche le ridotte della serie geometrica sono
  
  Dunque

Esempio: frazione generatrice di un decimale periodico.

Il numero decimale periodico può essere scomposto nel seguente modo

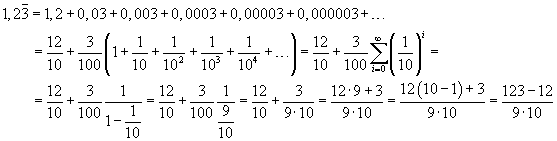
Risulta così giustificata la nota regola proposta spesso piuttosto dogmaticamente.