Nelle sezioni precedenti si è visto che, data una funzione reale di variabile reale f(x), se la funzione è derivabile infinite volte ed esiste il limite della funzione e delle sue derivate per x→0, è possibile individuare una serie S(x) convergente a f(x) per ogni x. Si può assumere viceversa che una serie S(x) convergente per ogni x sia sufficiente a definire una funzione f(x). Questo è il modo in cui L. Euler studiò inizialmente la somma delle potenze con esponente naturale n dei reciproci dei numeri naturali. Dopo di lui, B. Riemann estese il dominio di questa funzione anche alle potenze ad esponente complesso z con parte reale >1, per cui oggi questa funzione è nota come funzione ζ di Riemann. Successivamente la funzione è stata ridefinita in modo da estendere il suo dominio a tutto il piano complesso. In questa sede comunque ci si interessa solo di esponenti reali.
La funzione ζ (zeta) di Riemann è definita come
Limitando lo studio al caso di esponenti naturali ζ(n), se n=1, la (10.1) è la serie armonica, che non converge e, conseguentemente non converge per n<1.
I valori di ζ(n), se n è un numero naturale pari, possono essere dedotti esattamente. Un metodo può essere il seguente.
Si considera lo sviluppo in serie di MacLaurin del seno
Se x≠0, si ha
p(x) ha gli stessi zeri di sin x, escluso 0.
In generale, un polinomio P(x), con zeri non nulli xk e tale che P(0)=1, può essere fattorizzato in
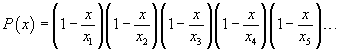
Quindi p(x) può essere scritto
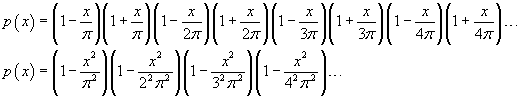
Per velocizzare il calcolo, sia
;
si ha
Lo sviluppo in serie di MacLaurin di p(α) è
La derivata prima di p(α) può essere calcolata usando il metodo della derivata logaritmica
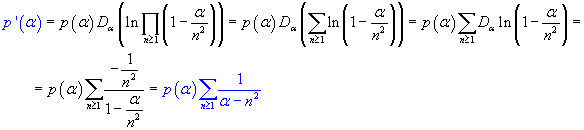
Per α=0 si ha
p'(0)α deve coincidere con
,
quindi
Infine si ottiene il valore di ζ(2)
Dato p'(α), si può calcolare p''(α)
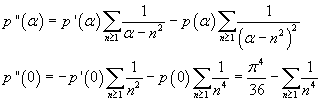
deve coincidere con
,
quindi
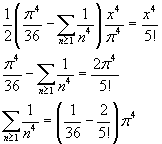
Il valore di ζ(4) è
Dato p''(α), si può ottenere p'''(α)
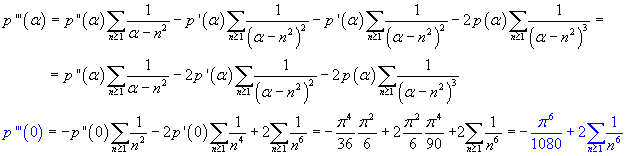
deve coincidere con
,
quindi
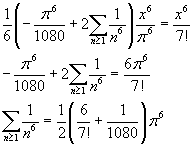
Il valore di ζ(6) è
Si osserva che valori di ζ per n naturale pari calcolati e i successivi che si potrebbero ottenere con lo stesso metodo possono essere ottenuti in funzione dei numeri di Bernoulli:
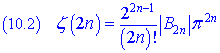
Se si assume la (10.2) come definizione della funzione ζ per argomenti naturali, si può ottenere un valore anche per n=0, caso in cui la definizione (10.1) diverge. Si ha
Il dominio di convergenza di ζ può essere ulteriormente esteso. Si può infatti dimostrare che per numeri naturali n≥2,
quindi
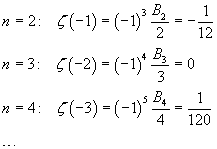
I numeri di Bernoulli con indice dispari ≥ 3 sono tutti 0, quindi i valori di ζ per argomenti interi negativi pari sono tutti 0.
Tabella di alcuni valori di ζ(n) generata da WolframAlpha
Per argomenti reali, i valori di ζ possono essere approssimati numericamente (P. Borwein in "An Efficient Algorithm for the Riemann Zeta Function").
La seguente applicazione Javascript permette di approssimare i valori di Z per argomenti reali.
Se il vostro browser non ammette il tag iframe potete aprire la pagina sorgente.