Integrali gaussiani

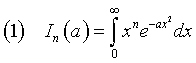
(a cura di Roberto Bigoni)

English version

Gli integrali del tipo

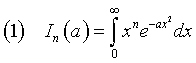
che si incontrano nella teoria della probabilità e nella teoria cinetica dei gas ideali, considerati come funzioni di a, sono caratterizzati dalla seguente proprietà

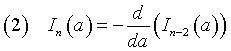
cioè

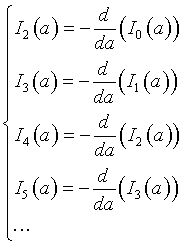
Quindi, una volta calcolati I_o(a) e I₁(a), i successivi si ottengono facilmente.

• Il calcolo di I₁ è abbastanza agevole.
  Si verifica facilmente che in questo caso la funzione integranda

  

  è la derivata rispetto a x di

  

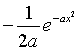
  quindi

  

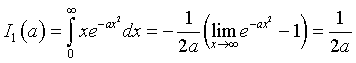
• Il valore di I_o, nel quale la funzione integranda è l'esponenziale

  

  può essere ottenuto nel seguente modo:

  1. si considera l'integrale della gaussiana su tutto ℜ sia sulla variabile x sia sulla variabile y

     

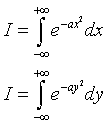
     quindi

     

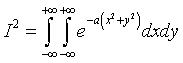
  2. nel piano Oxy alle coordinate cartesiane (x,y) si sostituiscono le coordinate polari (ρ,θ):

     

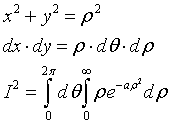
  3. il primo integrale vale 2π, il secondo è I₁, quindi

     

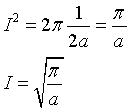
  4. data la simmetria della gaussiana, I₀ è la metà di questo valore: dunque

     

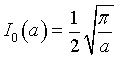
Si ottengono allora dalla (2)

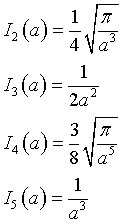
e così via.

In generale

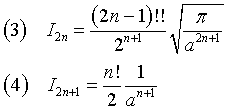
cioè

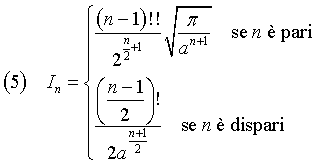
ultima revisione: Maggio 2018