Dato un insieme S di n elementi, questi possono essere utilizzati per comporre raggruppamenti Gi.
Il numero dei possibili raggruppamenti Gi è virtualmente infinito e virtualmente infinito può essere il numero dei loro elementi. Ma nelle situazioni operative vengono adottate in modo più o meno esplicito precise regole di formazione che ne limitano il numero in modo che questi raggruppamenti possano essere contati.
Ad esempio, dato l'insieme delle lettere dell'alfabeto latino, si possono costruire sequenze rappresentanti le parole della lingua inglese. Il numero delle parole possibili non è limitato a priori, né lo è la loro lunghezza: si possono teoricamente inventare neologismi o parole più o meno fantasiose, ma in generale, se si vuole che siano leggibili, la loro lunghezza non potrà essere arbitraria; anche dopo aver stabilito un lunghezza massima non tutte le sequenze possono essere ammissibili; quindi il numero delle parole in un vocabolario inglese è limitato, non solo dalla necessità che ogni parola abbia un significato, ma anche dalla compatibilità fonetica e ortografica. Ad esempio, è da escludere che una sequenza contenente hgtkx (a meno che non sia un particolare acronimo) venga inclusa in un vocabolario.
Il calcolo a priori del numero E dei raggruppamenti Gi è possibile solo se si stabilisce esplicitamente il
metodo da usare per la loro formazione. La trattazione formale di questo argomento, sviluppata nella seconda
metà del secolo scorso soprattuto da Gian-Carlo Rota,
è nota come Twelvefold way.
In questa sede ci si limita agli aspetti più elementari e intuitivi.
Il metodo più restrittivo consiste nell'imporre che i raggruppamenti Gi siano sottinsiemi di S tali da costituire una partizione di S, quindi
Questo caso viene trattato alla pagina Partizioni di questo sito.
Se invece si ammette che gli elementi di S siano tutti distinguibili e che i raggruppamenti Gi possano avere elementi in comune, il loro numero può essere limitato fissando il numero k degli elementi da essi contenuti.
In questo caso il loro numero risulta diverso a seconda del criterio che si adotta per valutare la distinguibiltà o meno di due raggruppamenti formati dagli stessi elementi.
Inoltre, se si formano gruppi prendendo solo una volta gli elementi di S, contiamo le permutazioni o combinazioni semplici; altrimenti contiamo le permutazioni o combinazioni con elementi ripetuti.
Allo scopo di facilitare il calcolo del numero di raggruppamenti possibili nei vari casi descritti, è utile introdurre la funzione fattoriale di un numero naturale n.
Dato un numero naturale n>0, il suo fattoriale, scritto n!, è il prodotto di tutti i numeri naturali 0 < i ≤ n.
![]()
Ovviamente
![]()
Se n>1, si ha
![]()
Volendo estendere la validità di questa uguaglianza anche al numero n=1, bisogna ammettere
![]()
Se k<n,
![]()
![]()
L. Euler ha esteso il calcolo della funzione fattoriale anche ad argomenti reali o complessi definendo la funzione Γ (Gamma).
Dato un insieme S di n elementi distinguibili, una permutazione semplice di classe k è una delle successioni che si possono formare prendendo una sola volta k elementi di S (k ≤ n). Il numero di queste successioni è scritto Pn,k.
In particolare, se si indica semplicemente con Pn il numero dei differenti modi di ordinare tutti gli elementi di S, si ha
![]()
Per induzione:
se si aggiunge un ulteriore elemento all'insieme S, da ogni successione Pn si possono ottenere n+1 nuove successioni distinguibili, ognuna di esse formata da n+1 elementi; quindi il numero di permutazioni Pn+1 è
![]()
Se gli elementi di S non sono tutti diversi tra di loro, ma, per esempio, S contiene m repliche dello stesso elemento, ci saranno m! permutazioni indistinguibili l'una dall'altra, che in effetti ne valgono una sola, per cui Pn,n va diviso per m!:
![]()
Se tutti gli elementi di S are sono diversi tra di loro e k<n, dato il numero Pn,k dei diversi ordinamenti di k elementi di S e il numero Pn-k dei diversi ordinamenti dei rimanenti n-k elementi, il numero Pn dei possibili ordinamenti di tutti gli elementi di S è dato da
![]()
e quindi
![]()
Ovviamente, se k=n, dall'uguaglianza (2.4) si ha
![]()
Nella manualistica italiana il termine permutazione denota in modo specifico uno dei possibili ordinamenti di tutti gli elementi di S per cui il simbolo P è specificato da un solo indice; se si ordinano solo k<n elementi si usa il termine disposizione e il simbolo Dn,k. Questa distinzione appare ridondante, per cui, in questa esposizione, si segue l'uso internazionale, in cui si parla solo di permutazioni.
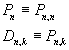
Dato un insieme S di n elementi distinguibili, una combinazione semplice di classe k è un sottinsieme di S formato da k (k≤n) dei suoi elementi, ognuno preso una sola volta. L'ordine degli elementi del sottinsieme non è rilevante. Il numero di questi sottinsiemi è scritto Cn,k.
Per calcolare Cn,k, si osserva che ognuno dei sottinsiemi di k elementi ammette k! permutazioni distinguibili, per cui
![]()
e quindi
![]()
I numeri Cn,k coincidono con i numeri del triangolo di Pascal (o Tartaglia), usato per lo sviluppo della n-esima potenza di un binomio, per cui essi sono usualmente denominati coefficienti binomiali e possono essere rappresentati nei seguenti modi
![]()
In questa esposizione n è denominato antecedente e k è denominato conseguente.
I coefficienti binomiali con lo stesso antecedente sono simmetrici, cioè
![]()
L'identità si ricava direttamente dalla (3.2).
Un coefficiente binomiale di antecedente n e conseguente k è uguale alla somma dei due coefficienti binomiali di antecedente n-1 e conseguenti k-1 e k.
Questa proprietà coincide con la regola di formazione del Triangolo di Pascal.
![]()
Infatti:
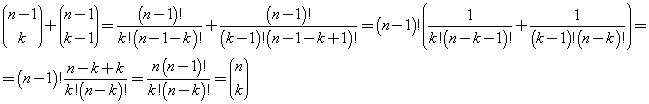
I coefficienti binomiali di antecedente n sono i coefficienti dello sviluppo polinomiale della potenza n-esima del binomio a+b.
![]()
La somma di tutti i coefficienti binomiali di uguale antecedente n è la potenza n-sima di 2.
![]()
La (3.6) segue immediatamente dalla (3.5) se si pone a = b = 1.
Se S è un insieme di n elementi distinguibili, il numero di tutti i suoi sottinsiemi distinguibili (compresi l'insieme vuoto e S stesso), cioè la cardinalità dell'insieme potenza P(S), è 2n.
Infatti i sottinsiemi di S sono tutte le possibili combinazioni semplici dei suoi elementi e la somma di tutte le combinazioni semplici è data dalla (3.6).
Se invece gli n elementi di S sono tutti indistinguibili l'uno dall'altro, il numero dei suoi sottinsiemi distinguibili coincide con il numero delle sue partizioni, che, in pratica, coincide con il calcolo delle partizioni del numero n.
Per n > 0 la somma a segni alterni dei coefficienti binomiali è 0.
![]()
La (3.7) segue immediatamente dalla (3.5) se si pone a = 1 e b = -1.
Per n > 0
![]()
Dato un insieme S di n elementi distinguibili, una permutazione con ripetizione è una successione formata prendendo k elementi di S, eventualmente anche più di una volta. k può quindi essere maggiore di n.
Queste permutazioni sono considerate distinguibili se sono formate da elementi diversi o, altrimenti, se i loro elementi sono ordinati in modo diverso.
Il numero di queste permutazioni è rappresentato dal simbolo P'n,k.
Per calcolarlo, si osserva che da ogni permutazione di k elementi, si ottengono n permutazioni con k+1 elementi aggiungendo ad essa ognuno degli n elementi di S.
Dato che
![]()
dall'uguaglianza (4.1) segue
![]()
In generale
![]()
Dato un insieme S di n elementi distinguibili, una combinazione con ripetizione è un insieme formato prendendo k volte elementi da S, ognuno di essi eventualmente anche più di una volta. k può quindi essere maggiore di n.
Tali combinazioni sono considerate diverse solo se hanno elementi diversi.
Il loro numero è indicato con C'n,k.
Questo numero è lo stesso che si avrebbe nel calcolo delle combinazioni semplici con k elementi presi da un insieme Sn+k-1 formato da n+k-1 elementi tutti diversi. Quindi dall'uguaglianza (3.2) si ottiene
![]()
Per esempio, dato l'insieme S = {a,b,c}, una possibile combinazione con k = 5 elementi è il gruppo {a,a,a,a,a} dove gli ultimi quattro a sono considerati come fossero elementi distinguibili.