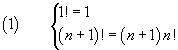
Il fattoriale n! di un numero naturale è definito ricorsivamente come
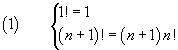
L. Euler trovò che è possibile definire una funzione di variabile reale (o complessa) Γ(x) ('Gamma di x') con la stessa proprietà di ricorsività
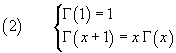
Se si applica questa funzione ad un argomento x+1 coincidente con un numero reale, si ottiene
Quindi Γ, per argomenti naturali, genera valori identici a quelli del fattoriale.
Euler riuscì ad esplicitare la funzione Γ in questo modo:
Infatti la definizione (4) dà
e anche
In particolare, se x coincide con il numero naturale n, si hanno le seguenti uguaglianze
Usando la seconda delle (2), dato
, si possono calcolare i valori
per ogni numero naturale
n ≥ 1.
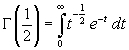
Ponendo t=z2, si ha
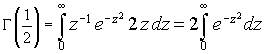
L'ultimo integrale è un noto
integrale gaussiano e ha valore
. Quindi
I valori di Γ per successivi incrementi di 1 dell'argomento possono essere ottenuti ricorsivamente
In generale, per n ≥ 0,
Nell'uguaglianza (8) il doppio punto esclamativo rappresenta il doppio fattoriale del numero naturale che lo precede, cioè, se il numero è dispari, il prodotto del numero stesso per tutti i dispari precedenti, e, se il numero è pari, il prodotto del numero stesso per tutti i pari precedenti. Si assume inoltre -1!! = 0!! = 1
Le uguaglianze (7) e (8) permettono di estendere la definizione del fattoriale dall'insieme dei naturali
all'insieme
nel seguente modo
In particolare
Dalla seconda delle uguaglianze (2) si ha inoltre
quindi
e ricorsivamente
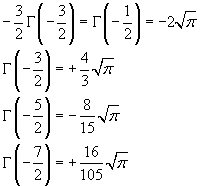
In generale, per n ≥ 0,
Si può quindi definire il fattoriale anche sull'insieme
nel seguente modo
In particolare
La seguente applicazione Javascript permette di approssimare i valori di Γ(x) per argomenti reali o complessi.
Se il vostro browser non ammette il tag iframe potete aprire la pagina dell'applicazione
In input, oltre alle cifre decimali, si possono usare le costanti P per π, E per le notazioni esponenziali e I per l'unità immaginaria.
La definizione del doppio fattoriale, in modo simile a quella del fattoriale, implica la seguente relazione ricorsiva
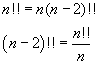
Se si applica questa proprietà a numeri minori di , si ottiene
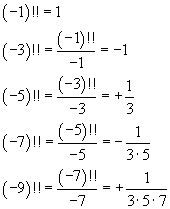
In generale, for n ≥ 1,
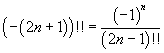
Quindi è possibile calcolare il doppio fattoriale di un numero intero negativo se il numero è dispari, ma non è possibile se il numero è pari perché il calcolo di (-2)!! implica una divisione per 0.
La (11) permette di calcolare
coefficienti binomiali del tipo
.
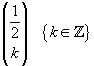Infatti, se si esprimono i coefficienti binomiali in termini di fattoriali, si ha
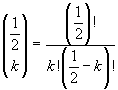
Se k=0, risulta immediatamente
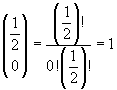
e, per k≥1
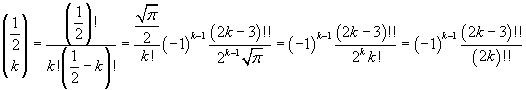
In particolare:
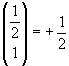
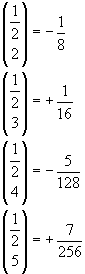
Se ora si confronta questa successione con la successione dei coefficienti delle potenze della variabile x nello sviluppo in serie di MacLaurin della radice quadrata di (1-x) (per x real e ≤1)
si osserva che le due successioni coincidono. Quindi
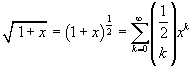
Questa identità è un esempio di come sia possibile applicare il teorema binomiale anche quando l'esponente del binomio non è un numero naturale.
Infatti, usando la funzione Γ, è possibile calcolare i coefficienti binomiali non solo se, come si è visto, il primo
termine è
, ma in generale quando il primo termine
è qualunque numero reale r o complesso z. Infatti, dato
G = Γ(r), si ha
e anche
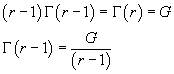
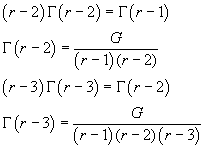
In generale, per n naturale ≥ 1,
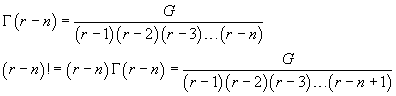
Infine
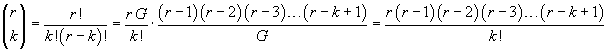
e, più sinteticamente,
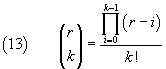
Esempi.
Interi negativi.
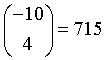
Razionali.
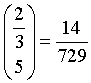
Reali.
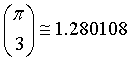
Complessi.
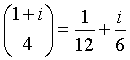
La (13) permette quindi di ottenere lo sviluppo in serie di varie funzioni di binomio evitando le derivazioni richieste dal metodo di Maclaurin.
La seguente applicazione Javascript permette di approssimare i valori dei coefficienti binomiali per argomenti reali.
Se il vostro browser non ammette il tag iframe potete aprire direttamente la pagina dell'applicazione
In input, oltre alle cifre decimali, si possono usare le costanti P per π, E per le notazioni esponenziali e I per l'unità immaginaria.
Se nell'integrale dell'identità (7) si pone
si ottiene
cioè
Se si moltiplica e divide la funzione integranda per en e si estraggono dall'integrale i fattori che non dipendono dalla variabile di integrazione y, si ha
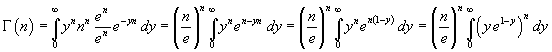
La derivata della funzione integranda
rispetto a y è
quindi f(y) ha un massimo assoluto per y=1. Allo scopo di approssimare il valore dell'integrale, si può esprimere l'integrale stesso come funzione di w = y-1
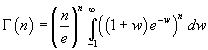
e quindi approssimare la funzione integranda f(w) nel seguente modo (da MathWorld):
si calcola il logaritmo della funzione
se n è sufficientemente grande, la funzione tende velocemente a 0 a destra e a sinistra del valore massimante, quindi si può assumere che il valore assoluto di w prossimo a 0; per valori w tali che |w|<1 si può sviluppare il logaritmo usando la serie di Mercatore
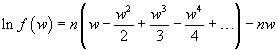
e quindi
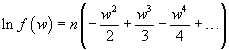
Se si tronca lo sviluppo al termine del primo ordine, si ha
cioè
La funzione Γ può essere approssimata da
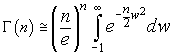
Dato che la funzionef(w) tende rapidamente a 0 in un intorno di 1, il valore di questo integrale non cambia apprezzabilmente se si estendono i limiti di integrazione da -∞ a +∞
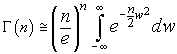
L'integrale a secondo membro è un
integrale gaussiano
e vale
;
quindi si ha
e in definitiva
La (14) è l'approssimazione di Stirling a n! e risulta utile in molte applicazioni probabilistiche e statistiche.
Per esempio:
per 10! invece del valore corretto 3628800 dà 3598697; l'errore è 8 ‰;
per 100! l'errore è 0.8 ‰;
per 1000! l'errore is 0.08 ‰.
È spesso utile calcolare il logaritmo del fattoriale. Dalla (15) si ha
Per n molto grandi, l'ultimo addendo è trascurabile e si può più semplicemente scrivere
La seguente applicazione Javascript permette di confrontare il valore esatto del fattoriale di un numero naturale
con quello ottenuto con l'approssimazione di Stirling.
Se il vostro browser non ammette il tag iframe potete aprire direttamente la pagina dell'applicazione.
