(a cura di Roberto Bigoni)
Molti teoremi matematici consistono nella dimostrazione che una determinata proprietà è valida per tutti gli elementi di un insieme universo prefissato: indicando l'universo con A, un suo generico elemento con a, la proprietà con P e usando il simbolismo logico si può scrivere:
![]()
Traducendo: "è sempre vero che, se a è un A, a gode della proprietà P".
Il più delle volte il processo di dimostrazione si basa sul metodo deduttivo: riferendosi ai postulati ed eventualmente anche a teoremi precedentemente dimostrati e applicando principi logici di validità generale, si conclude che la proprietà ha validità universale, cioè che vale per tutti gli elementi di A.
Ad esempio: "È sempre vero che se a è un triangolo, la somma dei suoi angoli interni è uguale ad un angolo piatto".
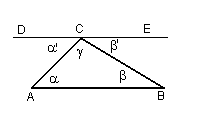 |
Sia ABC un triangolo qualunque e siano α, β e γ i suoi angoli interni. Si traccia per C la parallela ad AB (che esiste ed è unica:postulato). L'angolo DCA ha misura α'=α perché alterno interno rispetto a CAB (teorema). L'angolo ECB ha misura β'=β perché alterno interno rispetto a ABC(teorema). La somma di α'+γ+β' è uguale a DCE che è un angolo piatto di misura π. Poiché somme di grandezze uguali sono uguali (regola di validità generale) anche α+β+γ=π. |
Sono ammesse anche le dimostrazioni per assurdo: dovendo dimostrare la verità una proposizione, si dimostra che, se essa fosse falsa, se ne dedurrebbero risultati incoerenti, dunque la proposizione non può che essere vera.
Ad esempio: "I numeri primi sono infiniti".
Come è noto, i numeri primi sono i numeri naturali maggiori di 1 divisibili solo per se stessi e per 1.
Se i numeri primi non fossero infiniti, esisterebbe il massimo numero primo m e sarebbe possibile calcolare il numero p
uguale al prodotto di tutti i numeri primi: ![]()
Si consideri il numero naturale s immediatamente successivo a p:
![]()
è impossibile che s sia primo, perché maggiore del massimo primo m.
Dividendo s per qualunque numero primo fattore di p, si otterrebbe come quoziente il prodotto dei rimanenti numeri primi e resto 1 e quindi s non è divisibile per nessuno dei numeri primi considerati; dovrebbero allora esistere altri numeri primi, maggiori di m, ma anche questo è impossibile.
Se si ammette che esista il massimo numero primo m, si ottengono conclusioni contraddittorie. Bisogna pertanto ammettere che i numeri primi sono infiniti.
Altro famoso esempio di dimostrazione per assurdo: "La radice quadrata di 2 non è razionale".
I numeri razionali sono quelli che possono essere espressi come rapporto tra due numeri interi, cioè da frazioni. Dunque, se la radice di 2 fosse razionale si avrebbe
![]()
dove la frazione si suppone ridotta ai minimi termini, cioè m e n sono primi tra di loro.
Elevando al quadrato entrambi i termini dell'uguaglianza si ha
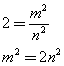
Il quadrato di m è pari, dunque anche m è pari e quindi è il doppio di un altro numero p. si ha quindi
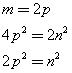
cioè anche il quadrato di n è pari e quindi anche n è pari. m e n devono essere entrambi pari, ma questa conclusione contrasta con l'assunzione che m e n siano primi tra di loro.
Se si ammette che la radice di 2 sia razionale si ottengono conclusioni contraddittorie, dunque bisogna ammettere che non è razionale.
Nella fondazione assiomatica dell'aritmetica i matematici operanti a cavallo tra Ottocento e Novecento, in particolare R. Dedekind e G. Peano, trovarono necessario ammettere un ulteriore metodo di dimostrazione, basato su un principio logico, detto principio di induzione matematica, valido per le successioni di proposizioni logiche.
Data un'applicazione
![]() , dove N
è l'insieme dei naturali e A un insieme prestabilito,
una successione in A è l'insieme degli elementi di A
corrispondenti in f ai numeri naturali.
, dove N
è l'insieme dei naturali e A un insieme prestabilito,
una successione in A è l'insieme degli elementi di A
corrispondenti in f ai numeri naturali.
Usualmente tutti gli elementi di una successione sono indicati dallo stesso simbolo a corredato da un indice che esprime il numero naturale corrispondente. L'indice va scritto come deponente, cioè con corpo tipografico più piccolo in basso a destra.
a1, a2, a3,....ai,...
ai è lo i-esimo elemento della successione.
L'intera successione può essere indicata nel seguente modo:
![]() .
.
Ad esempio, la successione dei numeri dispari (di)i ∈ N = {1,3,5,7,....} può essere efficacemente denotata da di=2i-1 dove d1=1, d2=3, d3=5,...
Una successione di proposizioni logiche
![]() è una successione di affermazioni con identico predicato p riferito ad espressioni
dipendenti da un numero naturale i.
è una successione di affermazioni con identico predicato p riferito ad espressioni
dipendenti da un numero naturale i.
Ad esempio:
è intuitivamente evidente che tutte le pi sono vere e che non tutte le qi sono vere, ma l'intuizione non è ammessa come metodo di dimostrazione: è necessario un procedimento formale di deduzione o di induzione riconosciuto come valido.
Il principio di induzione matematica risulta particolarmente efficace quando si tratta di dimostrare che un predicato p è vero se il soggetto è un qualunque elemento di una successione individuato dell'indice i.
|
Data una successione di proposizioni
logiche
allora tutte le p i sono vere. |
![]()
cioè: sommando un numero naturale (maggiore o uguale a 1) con il suo quadrato si ottiene un numero pari.
L'affermazione può facilmente essere dimostrata per deduzione. Infatti se n è pari, anche il suo quadrato è pari e si ha quindi la somma di due numeri pari che è pari; se n è dispari, anche il suo quadrato è dispari e si ha la somma di due numeri dispari che è pari. In tutti i casi il risultato è pari.
Usando il metodo di induzione matematica si procede nel seguente modo:
![]()
cioè il numero successivo a n più il suo quadrato è la somma di due numeri pari, dunque è pari.
![]()
cioè: sommando il cubo di un numero naturale (maggiore o uguale a 1) con il suo quintuplo si ottiene un multiplo di 6.
Anche in questo caso l'affermazione può essere dimostrata per deduzione.
Infatti, la somma indicata o è la somma di due numeri pari o è la somma di due numeri dispari:
in entrambi i casi risulta pari. Basta quindi dimostrare che è anche multipla di 3.
Questo è direttamente verificabile per
n=1 o n=2. Per ogni altro n ≥ 3 si ha
![]()
in cui la tesi è ovvia se n è un multiplo di 3.
In caso contrario, o (n-2) o (n+2) è un multiplo di 3 e quindi anche il loro
prodotto è multiplo di 3.
Si può quindi porre
![]() e ottenere
e ottenere
![]() evidenziando
così che la somma è multipla anche di 3.
evidenziando
così che la somma è multipla anche di 3.
Usando il metodo di induzione matematica si procede nel seguente modo:
![]()
![]() è
la somma di due multipli di 6, dunque è multiplo di 6.
è
la somma di due multipli di 6, dunque è multiplo di 6.
![]()
cioè: la somma nei primi n numeri naturali dispari è uguale al quadrato di n
L'affermazione è vera se n è 1.
Ammettendo che sia vera per i primi n dispari, bisogna dimostrare che è vera anche se si estende la somma al numero dispari successivo, cioè che
![]()
Dimostrazione:
![]()
![]()
cioè: la somma dei quadrati dei numeri naturali da 1 fino ad un certo numero n è uguale ad un sesto del prodotto tra n, il suo successivo e il suo doppio più 1.
è facile vedere che questa proprietà è valida se ci si ferma a 1.
Ammettendo la validità di questa proprietà per qualunque n, bisogna mostrare che è valida anche per n+1, cioè che
![]()
Dimostrazione:
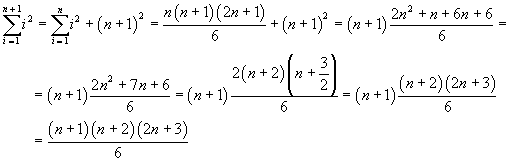
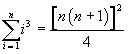
cioè: la somma dei cubi dei numeri naturali da 1 fino ad un certo numero n è uguale ad un quarto del quadrato del prodotto tra n e il suo successivo.
è facile vedere che questa proprietà è valida se ci si ferma a 1.
Ammettendo la validità di questa proprietà per qualunque n, bisogna mostrare che è valida anche per n+1, cioè che
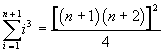
Dimostrazione:
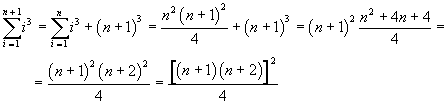
Un'interessante variante della stessa identità è la seguente
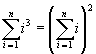
cioè
![]()
Infatti, nell'uguaglianza
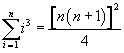
il secondo membro può essere scritto come
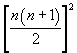
ed è facile dimostrare che la base del quadrato è la somma di tutti i numeri naturali da 1 a n.
![]()
Se n=1, l'uguaglianza si riduce a
![]() .
.
Ammettendo la validità dell'uguaglianza per n, deve risultare vero che
![]()
Dimostrazione:
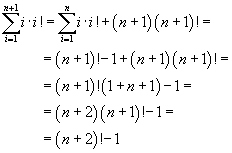
Serie di Mengoli.
![]()
L'uguaglianza è immediatamente verificata per n=1.
Ammettendo l'identità per n si ottiene
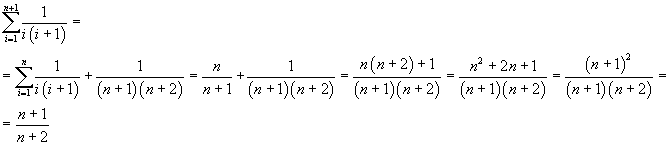
L'identità vale anche per n+1, dunque vale in generale.
![]()
cioè: la somma delle potenze successive della base a da 1 fino ad un certo esponente n è uguale al prodotto della base per il rapporto tra la differenza tra 1 e la potenza n-esima della base e la differenza tra 1 e la base.
è facile vedere che questa proprietà è valida se ci si ferma a 1.
Ammettendo la validità di questa proprietà per qualunque n, bisogna mostrare che è valida anche per n+1, cioè che
![]()
Dimostrazione:
![]()
![]()
cioè: la derivata della potenza n-esima della base x è data dal prodotto dell'esponente n per la precedente potenza della base.
è facile vedere che questa proprietà è valida per n=1.
Ammettendo la validità di questa proprietà per qualunque n, bisogna mostrare che è valida anche per n+1, cioè che
![]()
Dimostrazione:
![]()
Applicando la regola di derivazione di un prodotto:
![]()
Corollario
Scrivendo l'uguaglianza precedente nella forma
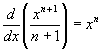
si osserva che, a sua volta, la potenza n-esima della variabile x è la derivata del rapporto tra la potenza successiva e il suo esponente. Si dirà che tale rapporto è l'antiderivata fondamentale di xn.
Ma la derivata di qualunque funzione ottenuta aggiungendo una costante k
all'antiderivata fondamentale è uguale a xn. L'insieme di tutte
queste funzioni è detto integrale indefinito: quindi l'integrale indefinito
di xn è
![]()
Questa relazione è normalmente indicata nel seguente modo:
![]()
![]()
Questa identità può essere dimostrata direttamente applicando il
teorema binomiale: infatti
![]()
Può essere tuttavia interessante dimostrarla per induzione. è infatti immediato verificare che vale per n=1. Per n+1 qualsiasi si ha
![]()
Osservando che
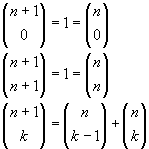
si ottiene
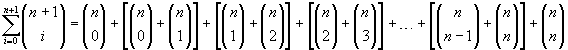
cioè
![]()
Corollario
Se un insieme I comprende n elementi distinti, il numero di tutti i suoi sottinsiemi (compreso l'insieme vuoto e
e I stesso), cioè la cardinalità dell'insieme potenza,
è 2n.
Infatti i sottinsiemi di I sono tutte le possibili combinazioni semplici dei
suoi elementi e la somma di tutte le combinazioni semplici è data dalla (10).
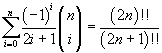
dove il doppio punto esclamativo dopo un numero naturale indica il doppio fattoriale del numero stesso, cioè, se il numero è pari, il prodotto di tutti i numeri pari che lo precedono e, se il numero è dispari, il prodotto di tutti i numeri dispari che lo precedono. Come per i fattoriali si assume 0!!=1
è immediato verificare che, per n=0 entrambi i membri valgono 1.
Assumendo valida l'identità proposta, bisogna dimostrare che
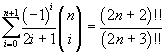
Se, per semplificare l'esposizione, si assume
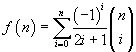
per ogni n>0, bisogna dimostrare che
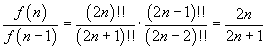
A questo scopo si osserva che
![]()
e anche, assumendo ![]() ,
,
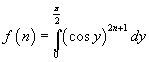
L'antiderivata della funzione integranda si può sviluppare per parti
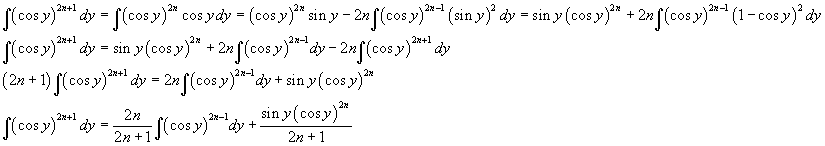
Calcolando l'integrale definito si ottiene quindi
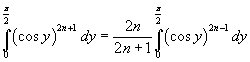
L'integrale a secondo membro è f(n-1). Dunque, in definitiva,
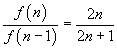
Con n=0, il primo membro è
Il secondo membro è
![]()
Dunque l'identità proposta vale per n=0. Assumendo valida l'identità, bisogna dimostrare che
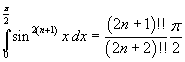
Calcolando per parti l'antiderivata della funzione integranda a primo membro si ha
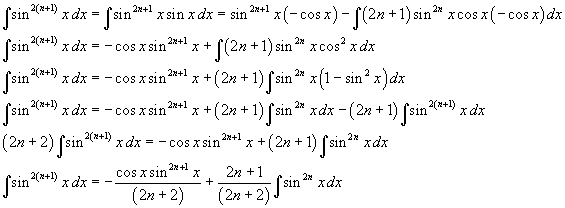
L'integrale definito risulta quindi
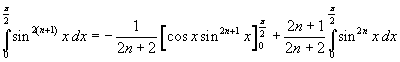
A secondo membro il primo addendo è nullo e l'integrale nel secondo è il primo membro della (12). Dunque
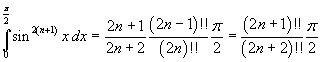
Quindi la (12) vale per ogni n.
Se, data una circonferenza, si considerano 2 punti su di essa e si traccia la corda avente estremi nei due punti, la circonferenza viene suddivisa in 2 regioni.
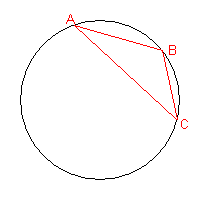
Se si considerano 3 punti e si tracciano tutte le possibili corde aventi per estremi ogni possibile coppia di punti, la circonferenza viene suddivisa in 4 regioni.
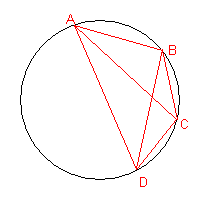
Se si considerano 4 punti e si tracciano tutte le possibili corde aventi per estremi ogni possibile coppia di punti, la circonferenza viene suddivisa in 8 regioni.
Se si considerano 5 punti e si tracciano tutte le possibili corde aventi per estremi ogni possibile coppia di punti, evitando che nei punti interni alla circonferenza si intersechino più di due corde, la circonferenza viene suddivisa in 16 regioni.
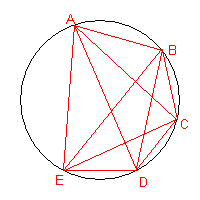
L'intuizione induce a prevedere che, aggiungendo un altro punto, sempre evitando che nei punti interni alla circonferenza si intersechino più di due corde, il cerchio risulterà suddiviso in 32 regioni. Ma non è vero: sono 31.
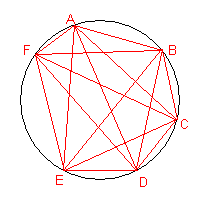
Come suggerito da D. Acheson nel volumetto "1089 e altri numeri magici" (Zanichelli - 2009), il numero di queste regioni è
![]()
La successione corretta può essere ottenuta osservando che, dato r1=1,
![]()
Aggiungendo un nuovo punto sulla circonferenza, si ottiene un aumento nel numero di regioni dato dalla somma tra il numero precedente di triangoli con vertici sulla circonferenza, espresso dal coefficiente binomiale, più il numero precedente di punti.
Ad esempio, nel passaggio da 4 a 5 punti rappresentato nella seguente figura
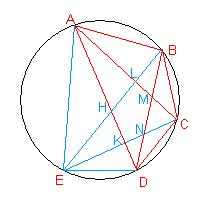
l'aggiunta del punto E produce:
In definitiva, passando da 4 a 5 punti si ha un aumento di 8 regioni.
| n | rn | rn-rn-1 | |
|---|---|---|---|
| 1 | 1 | ||
| 2 | 2 | 1 | 1 |
| 3 | 4 | 2 | 2 |
| 4 | 8 | 4 | 4 |
| 5 | 16 | 8 | 8 |
| 6 | 31 | 15 | 15 |
| 7 | 57 | 26 | 26 |
| 8 | 99 | 42 | 42 |
| 9 | 163 | 64 | 64 |
| 10 | 256 | 93 | 93 |
Quindi la relazione (1), può essere dimostrata per induzione. In fatti essa è vera per n=1 e, assumendola vera per un n successivo, si ottiene
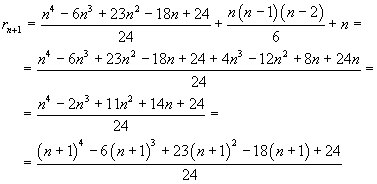
Quindi la (1) vale per ogni n.
ultima revisione: 23/04/2015