Geometrical Optics
(notes edited by Roberto Bigoni)
Basic principles.
Some optical phenomena can be explained, at least in their fundamental aspects,
by constructing geometric models based on the following principles.
Every point of a luminous source in homogeneous transparent medium emits signals
that spread in all the radial directions in straight lines;
the path of everyone of these signals is a light ray.
-
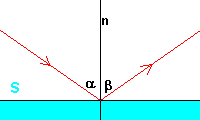
A ray that hits a perfectly reflecting surface S, i.e. the surface of a mirror,
bounces forming, with respect to the normal line (that is the perpendicular) n to the
surface in the incidence point, a reflection angle β equal to the angle of
incidence α.
The speed of the radiation is different in different transparent media;
it has its maximum in vacuum;
the speed in the vacuum is usually indicated by c.
-
A ray that hits the surface of separation between two different transparent media
A and B, in which it propagates with respective speeds vA
and vB splits in two rays: the one is reflected like in the previous case,
the other deflects from its rectilinear trajectory so that it forms, with respect to
the normal to the surface in the incidence point, angles α and β
such that
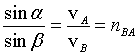 (Snell's law).
(Snell's law).
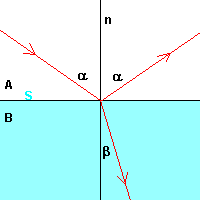
The ratio nBA is said the relative refractive index of B
with respect to A; if A is the vacuum, the ratio nBA
is said the absolute refractive index of B and can be indicated simply by
nB.
The refractive index depends not only on the transparent medium, but also on the color
of the ray: therefore rays having different colours in the same medium are refracted
in different ways.
Given α and nBA from the Snell's law we have
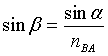 ;
if nBA≤sinα (that is if the second medium is sufficiently faster
than the first one), we have sinβ≥1.
The mathematical impossibility corresponds to the physical impossibility of the refraction:
in this case the incident ray is totally reflected;
the surface behaves like a mirror.
;
if nBA≤sinα (that is if the second medium is sufficiently faster
than the first one), we have sinβ≥1.
The mathematical impossibility corresponds to the physical impossibility of the refraction:
in this case the incident ray is totally reflected;
the surface behaves like a mirror.
Mirrors
-
When two rays, emitted from the same point A of a source, after their reflection by
a mirror, converge in the same point A', placed in the same side of A
with respect to the mirror, and reemerge from A', they behave exactly as they were
emitted from A'. A' is the image of A.
In this case the image A' is said to be real.
If instead two rays emitted from the same point A of a source, after having been
reflected by a mirror, diverge, their extensions beyond the specular surface converge in
the same point A'. The reflected rays are perceived like if they were emitted
from A'. A' is said to be the virtual image of A.
The set of all the points A' form a complete image of the source.
The plane mirrors produce always virtual images.
-
The mirrors formed by spherical cap of great radius, can be of two types:
- introverted (concave spherical mirrors);
- extroverted (convex spherical mirrors).
In the concave mirrors the rays parallels to the optical axis, that is the straight
line from the center C of the sphere to the vertex V of the spherical cap,
and very close to this axis (paraxial rays), after the reflexion by the mirror,
converge in the same point F, intermediate between C and V: this is a
real focus.
Vice versa, all the paraxial rays which, after their emission, pass through the focus,
are reflected parallelly to the optical axis.
All the rays passing for C have null angles of incidence and reflection:
they reemerge on themselves.
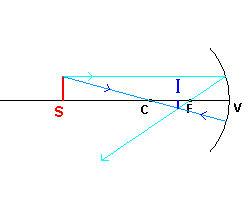
By analyzing the convergence of the reflections of two of this rays or of their
extensions we can obtain a real image or a virtual image.
Far from ideal condition (great radius, paraxial rays) the focus does not exist.
Between C and V there is only a place where the rays are very close each other:
this is a reflection caustic. The images aren't tidy because of spherical
aberrations.
In the ideal convex mirrors the focus is virtual and also the images are always virtual.
Dihedrons (prisms)
If a transparent optical medium is delimited by two plane surfaces
which forms an angle φ, a beam which penetrates in it from the outside, is,
usually, refracted twice in the same direction.
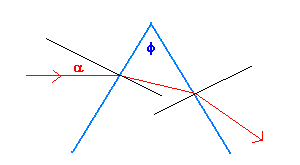
In the same optical medium different colours have different refractive indexes,
therefore, rays of different colour having the same angle of incidence, undergo different
deflections. If a beam, like as an example the white light, is a mixture of many rays
of different colours, every ray is bent on a different path.
The prism can therefore analyze a composed beam producing its spectrum.
Vice versa, if we can know the angle of deflection of a colour, we can determine its
refractive index.
If the angle between two surfaces of an optical medium is null, that is the two
surfaces are parallel, the dihedron is effectively a slab;
the two successive refractions of a beam neutralize each other and the final
deflection of the beam is null, that is the escape direction is parallel to the entrance
direction.
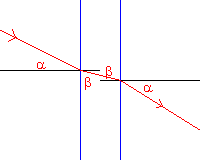
Spheres
In an optical medium with index of refraction n>1, delimited by a spherical surface with center at O,
a light beam AB coming from the outside has an angle of incidence i and a refractive angle r with respect to the radius OB.
The refracted part of the beam hits the surface at C with angle of incidence r and a part of it is reflected with reflection angle r.
In turn this part hits the surface at D, always with angle of incidence r, and is refracted outside with refractive angle r'
with respect to the radius OD. So a portion of a beam with direction AB from behind of those who observe the sphere, is seen by the observers as coming from the sphere with direction DE.
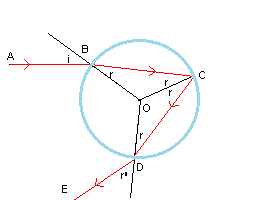
This model allowed Descartes to account for some of the main physical characteristics of the rainbow.
Lenses
An optical medium delimited by two coaxial spherical caps is a spherical lens.
The common axis of the two caps is then optical axis of the lens.
If a lens is thin, all the parallel paraxial monochromatic rays (that is the rays of
the same colour, parallel to the optical axis and very close to it), after
the passage through the lens, can
- converge in the same point F (the focus): the lens is
a converging lens and has a real focus;
- diverge so that their extensions converge in the same point F:
the lens is a diverging lens and has a virtual focus;
In the hypothesis of a thin lens, we can assume that between the vertexes of the caps
the surfaces of the lens are parallel: near this place the lens behaves like a slab.
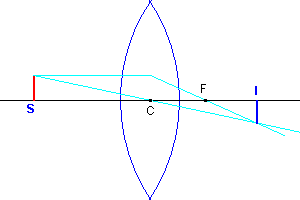
Saying C (center) the intermediate point between the vertexes,
we can therefore assume that the rays passing through C do not bend.
Given a point S (the source) and tracing from it the ray parallel to the optical axis and the ray passing through C, if the rays emerging from the lens converge,
the point I in which they converge is the real image of S.
If instead the rays emerging from the lens diverge, the point I in which their
extensions converge is the virtual image of S.
If a lens isn't thin or the rays aren't paraxial there will be, like in the mirrors,
spherical aberrations.
Because of the difference in the refractive indexes of the different colours, every
colour has its own focus: a lens shows also chromatic aberrations.
Undulatory optics
The principles of the geometrical optics can not account for other important phenomena shown by the light, that is,
interference and
diffraction.
To explain these phenomena you need to interpret a ray of light as the propagation of a
sine wave of an electromagnetic field.

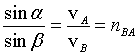 (Snell's law).
(Snell's law).
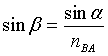 ;
if nBA≤sinα (that is if the second medium is sufficiently faster
than the first one), we have sinβ≥1.
The mathematical impossibility corresponds to the physical impossibility of the refraction:
in this case the incident ray is totally reflected;
the surface behaves like a mirror.
;
if nBA≤sinα (that is if the second medium is sufficiently faster
than the first one), we have sinβ≥1.
The mathematical impossibility corresponds to the physical impossibility of the refraction:
in this case the incident ray is totally reflected;
the surface behaves like a mirror.



