1. Plastic section and plastic number.

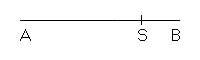
In a way analogue to that done in the golden section of a segment we can make the plastic section of a segment AB by finding its point S such that the cube with edge AS is equivalent to the rectangle parallelepiped with sides AB, SB and AB + AS.

This definition is due to the Benedictine architect-monk Hans Van der Laan(1904-1991) which he applied to some of his projects.

If you indicate with λ the measure of the segment AB and with σ the measure of the segment AS you have

thet is equivalent to

Let x be the ratio between λ and σ. You have

If you now represent in the same Cartesian plane the curves with equations y=x³ and y=x+1 you observe that they intersect in a single point with abscissa between 1 and 2: therefore the equation admits a unique real solution.

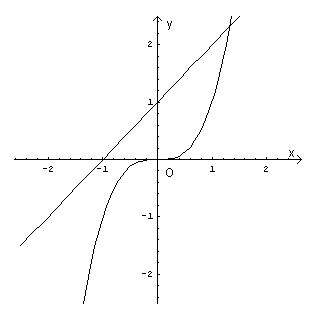
The real solution of the equation is called plastic number or plastic constant and, here, this number is denoted by P. The equation is called "plastic equation".

To calculate P you can solve the plastic equation with the method of Cardano by proceeding as follows

You rewrite the equation using the variable w

You obtain

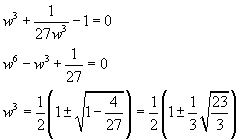
So the real roots of the equation in w are

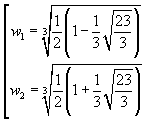
For simplicity, complex roots are omitted. By replacing one any of the two values w₁ and w₂ in the expression of x, with a calculator, you obtain an approximation to the solution P of the equation:

P≈1.3247179572447460...