(note a cura di Roberto Bigoni)

Data una fune sottile, inestensibile e perfettamente flessibile, appesa ai punti A e B, in condizione di equilibrio nel campo costante terrestre g, tale fune assume una configurazione descrivibile con una curva piana detta catenaria.
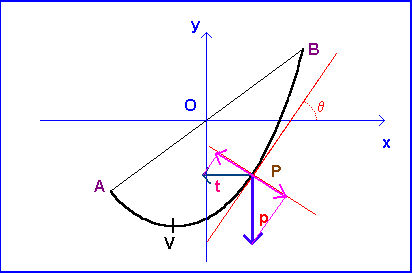
Per dedurre analiticamente l'equazione di tale curva, si scelga un sistema di riferimento cartesiano ortogonale avente origine nel punto medio di AB, asse delle ascisse orizzontale e asse delle ordinate verticale.
Si consideri un punto P sull'arco VP. Sull'elemento puntiforme di fune in posizione P, di lunghezza dl e massa dm, agiscono due forze:
La condizione di equilibrio del punto P è dovuta al fatto che la somma delle componenti tangenziali di t e p è equilibrata dalla reazione vincolare della fune, mentre le componenti di p e t perpendicolari alla tangente si equilibrano a vicenda e quindi i loro moduli sono uguali.
Detto θ l'angolo che la tangente al punto P forma con l'asse delle ascisse, si avrà
![]()
![]()
Detta y(x) l'equazione della curva che descrive la disposizione della fune nel sistema di riferimento scelto e dette x e y le coordinate cartesiane del generico punto P in tale sistema, la tg θ è data dalla derivata della y(x):
![]()
Il peso p è dovuto al peso del tratto VP della fune.
Dette v l'ascissa del vertice, λ la densità lineare della fune e g il modulo dell'accelerazione di gravità, il modulo del peso p è dato da
![]()
e quindi
![]()
Derivando entrambi i membri della (5)
![]()
E quindi
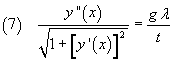
Posto
![]()
l'equazione differenziale (7), ammette come soluzione
![]()
Il simbolo cosh denota il coseno iperbolico
Note le coordinate a e b di B (e quindi le coordinate di A, simmetrico di B rispetto all'origine O) e la lunghezza L della fune (che ovviamente deve essere maggiore di AB), si ha
![]()
![]()
Dalla (10) si ottiene
![]()
e dalla (11)
![]()
Dividendo membro a membro la (12) per la (13)
![]()
E la funzione (9) può essere espressa
![]()
Dalla (14) si desume inoltre
![]()
Sostituendo la (16) nella (12) si ottiene
![]()
Noti a, b e L, l'equazione (17) permette di determinare il valore di k (diverso dalla soluzione banale 0!).
Poiché y(a)=b, dalla (15) si ha
![]()
Azzerando la derivata della y(x) nella (15)
![]()
L'ascissa v del vertice V risulta
![]()
L'ordinata di V risulta quindi
![]()
Il modulo T della tensione cui è sottoposto un elemento di fune di ascissa x può essere dedotta applicando il teorema di Pitagora ai moduli dei vettori p e t. Dalle (8), (3) e (9) si ha
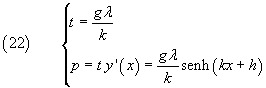
Quindi
![]()
![]()
ultima revisione: maggio 2018