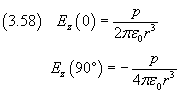Si definisce flusso elementare di un campo vettoriale h attraverso una superficie infinitesima dS il differenziale
dove con n si indica il versore normale alla superficie stessa. In particolare, se S delimita un volume V, si assume n orientato dall'interno del volume verso l'esterno.
In questo ultimo caso, se la superficie S racchiude un volume infinitesimo dV, senza perdita di generalità, essa può essere schematizzata come una superficie cubica con le facce parallele ai piani definiti dagli assi cartesiani
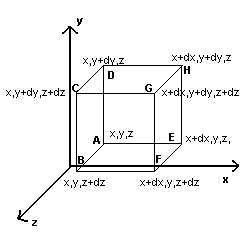
Il flusso del vettore h attraverso questa superficie è la somma dei flussi attraverso alle sei facce.
Considerando le due facce parallele al piano yz:
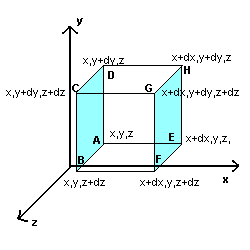
la componente di h in direzione i nel punto E è
In definitiva, il flusso di h attraverso queste due facce risulta
Ragionando in modo analogo sulle altre due coppie di facce, si ottiene che il flusso totale attraverso la superficie cubica è
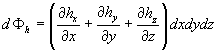
La somma tra parentesi può essere interpretata come il prodotto scalare tra
e h
e viene detta divergenza di h nel punto (x,y,z).
Il prodotto dei differenziali dxdydz è l'espressione del volume infinitesimo dV. Si ottiene dunque
Questo risultato è noto come teorema della divergenza o di Gauss.
In particolare, se h è il campo elettrico E
Se
si assume come principio fondamentale di elettromagnetismo che
dalla (3.3) si ottiene
e infine, indicando con
la densità di carica elettrica nel volume dV
La (3.5) esprime in forma differenziale uno dei quattro princìpi fondamentali dell'elettromagnetismo posti alla base della sistemazione teorica data da Maxwell, noti come equazioni di Maxwell.
Per la (2.5) si ha inoltre
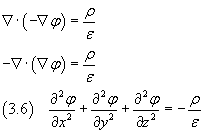
Introducendo l'operatore Δ
detto Laplaciano, la (3.6) può essere scritta
La (3.8) è nota come equazione di Poisson.
Ovviamente tutta la discussione ha senso solo se si assume φ derivabile a tratti almeno due volte rispetto alle coordinate spaziali. E dato che la derivabilità implica la continuità φ e E sono funzioni continue.
Si assume come principio fondamentale di elettromagnetismo che non esistono cariche magnetiche, quindi, se B è un campo di induzione magnetica, il flusso di B uscente da una superficie chiusa è nullo e conseguentemente è nulla la sua divergenza
Anche la (3.9) è una delle equazioni di Maxwell.
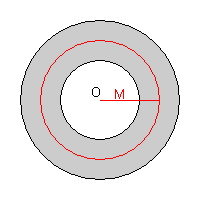
Uno strato sferico di raggio medio M e spessore 2fM, con f reale
positivo ≤ 1, posto nel vuoto, contiene una carica Q omogeneamente distribuita all'interno del suo volume
.
La densità di carica ρ nello spessore dello strato è
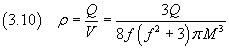
mentre all'esterno e nella cavità interna ρ è nulla.
In qualunque sistema di riferimento cartesiano con origine O nel centro dello strato, per la simmetria centrale del sistema il potenziale in un punto P in posizione r dipende solo dalla distanza r di O da P. Per i punti dello strato si ha quindi
Assumendo nullo il potenziale nei punti della superficie sferica di raggio R, la (3.11) ammette soluzione
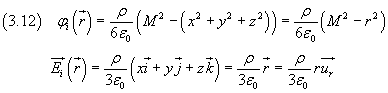
All'esterno dello strato la densità di carica è nulla. L'equazione di Poisson ammette come soluzione
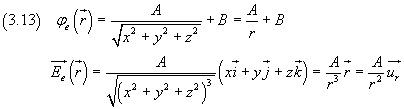
Dalla continuità di φ e E nei punti sulla superficie esterna dello strato, cioè per r=(1+f)M, si ha
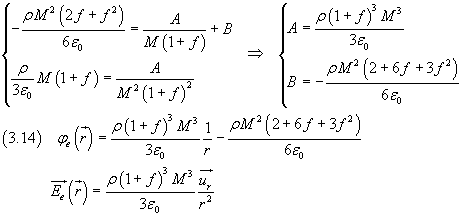
Per i punti interni alla cavità una soluzione del tipo della (3.13) è improponibile perché in O si avrebbe una singolarità. Δφ è nullo se φ è costante in tutta la cavità con valore coincidente con φi((1-f)R,0,0).
In conclusione:
nello strato il potenziale e campo sono espressi dalle (3.12)
all'esterno potenziale è espresso dalla (3.14) e il campo è
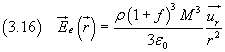
Per la (3.14) il potenziale a distanza infinita risulta
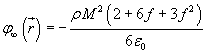. Se invece si assume che il potenziale
a distanza infinita sia nullo, tutti i potenziali ottenuti vanno aumentati di
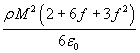. In particolare, il potenziale nella cavità
risulta
e i potenziali interno ed esterno
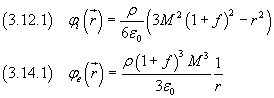
Se nelle uguaglianze (3.12), (3.14), (3.15) e (3.16) si pone f=1, si ottiene una sfera piena di raggio R=2M. In questo caso, assumendo nullo il potenziale all'infinito, si ha
dalla (3.12.1)
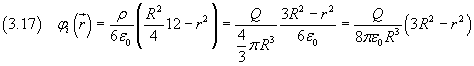
in particolare, per r=0, cioè nel centro della sfera piena di raggio D,
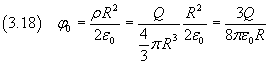
dalla (3.14.1)
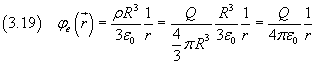
dalla seconda delle (3.12)
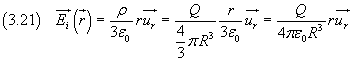
dalla seconda delle (3.14)
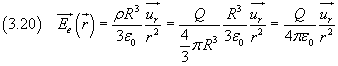
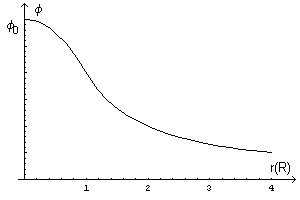
Esempio.
In prossimità della superficie terrestre si misura un campo elettrico E diretto verso il basso (cioè
verso il centro della Terra) di intensità
. Considerando la Terra come un
corpo sferico di raggio
, si deduce che la Terra
contiene una carica negativa
Assumendo nullo il potenziale all'infinito, il potenziale elettrico alla superficie della Terra risulta
Normalmente nella pratica elettrotecnica si assume nullo il potenziale alla superficie della Terra,
in modo da attribuire potenziale nullo anche a tutti i conduttori collegati alla Terra. Questa scelta equivale a porre
Tutti i conduttori di dimensioni trascurabili rispetto a quelle della Terra, indipendentemente dal fatto che inizialmente siano carichi o scarichi, una volta collegati a terra formano un unica entità con essa. In particolare ne assumono il potenziale e la densità superficiale di carica.
Una sfera conduttrice S di raggio RS=1m, collegata a Terra, è allo stesso potenziale della Terra e assume la stessa densità superficiale di carica della Terra
La carica su S può essere stimata moltiplicando questa densità per la superficie di S=4π m2:
Se nelle uguaglianze (3.12), (3.14), (3.15) e (3.16) si pone f=0, si ottiene uno strato sferico raggio R=M e spessore nullo. Detta σ la densità superficiale di carica nello strato, si ha
La densità volumica media di carica nella sfera delimitata dallo strato è
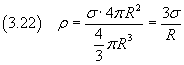
Assumendo nullo il potenziale all'infinito e f=0
dalla (3.16), il campo esterno è
dalle (3.15.1) e (3.14.1) i potenziali interno ed esterno allo strato risultano
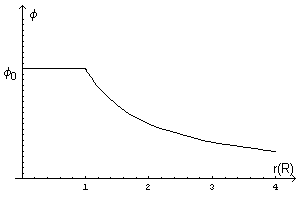
All'esterno dello strato, le espressioni del potenziale e del campo coincidono con la (3.19) e (3.20), cioè potenziale e campo sono identici a quelli che si avrebbero se tutta la carica fosse uniformemente distribuita all'interno della sfera.
Un tubo ideale di lunghezza infinita di raggio medio M e spessore 2fM,
con f reale positivo ≤ 1, posto nel vuoto, per ogni unità di lunghezza contiene una carica λ,
omogeneamente distribuita all'interno dello spessore.
Ogni porzione di lunghezza L di tale tubo contiene una carica Q=λL;
il volume della porzione è
;
quindi la densità di carica ρ all'interno del cilindro è
mentre all'esterno del tubo e nella sua cavità interna ρ è nulla.
Dato un punto P, per la simmetria assiale del sistema, si può assumere come origine O di un sistema di riferimento cartesiano la proiezione di P sull'asse del tubo e come asse delle z l'asse del tubo. Il potenziale in un punto P dipende solo dalla distanza r di P da O. Per la (3.8) se P è all'interno dello spessore del tubo si ha
Assumendo nullo il potenziale sulla superficie cilindrica di raggio M, la (3.26) ammette soluzione
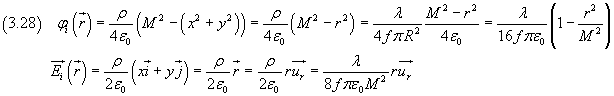
Per un punto esterno al tubo una soluzione è
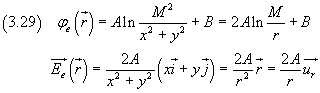
Per la continuità di φ e E nei punti sulla superficie esterna del tubo, cioè per r=(1+f)M, si ha
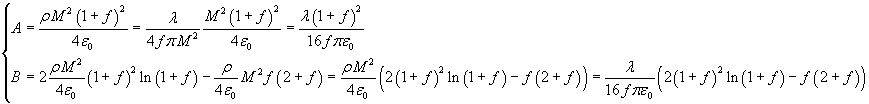
Come nel precedente caso dello strato sferico, il potenziale φ0 nella cavità interna va assunto uniformemente uguale a φi((1-f)M,0).
In conclusione:
nello strato potenziale e campo sono espressi dalle (3.28);
all'esterno il potenziale è
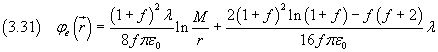
e il campo
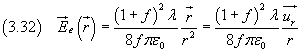
Sostituendo M con R/2, si ottengono potenziali e campi in funzione del raggio R del cilindro.
Dalla (3.30)
Dalle (3.28)
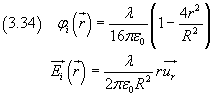
Dalle (3.31) e (3.32)
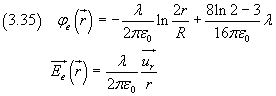
In particolare, alla superficie del cilindro, si ottiene
Assumendo nullo il potenziale φR, tutti i potenziali vanno aumentati di
, quindi
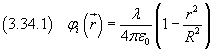
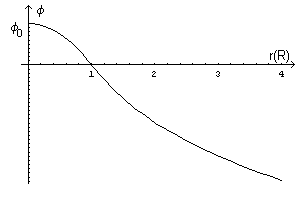
Assumendo f=0, un tubo cilindrico si riduce ad una superficie cilindrica ideale priva di spessore di raggio R=M. In questo caso la densità superficiale di carica σ si ottiene dividendo la carica Q presente su un tratto di strato di lunghezza L per la superficie del tratto stesso:
Se, come nel caso precedente, si assume nullo il potenziale sulla superficie, dato che nella cavità il potenziale è costante, per la continuità di φ, il potenziale è nullo in tutta la cavità.
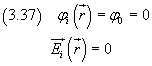
All'esterno, dalle (3.35),
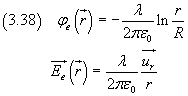
In una lastra piana ideale di estensione infinita e di spessore D, cioè un corpo delimitato da due piani paralleli distanti D l'uno dall'altro, posta nel vuoto, ogni unità di superficie contiene una carica σ, omogeneamente distribuita all'interno dello spessore e il volume sottostante ad ogni porzione di superficie S di tale lastra contiene una carica Q=σS.
Il volume della porzione è
;
quindi la densità di carica ρ all'interno della lastra è
Assumendo come origine O di un sistema di riferimento cartesiano un punto qualunque a metà dello spessore della lastra e come asse z la perpendicolare alla lastra per O, data l'arbitrarietà di O, potenziale e campo dipendono solo dalla componente z. Per la (3.6) all'interno della lastra si ha
che, assumendo nullo il potenziale nel piano centrale della lastra, ammette soluzione
All'esterno della lastra la densità è nulla, dunque
che ammette come soluzione
dove A e B sono grandezze costanti. Imponendo la continuità di φ e della sua derivata sulle superfici, cioè per z=±D/2, si ha
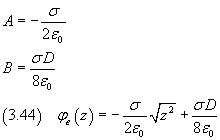
In conclusione
all'interno della lastra il campo è
all'esterno il campo è
Se la lastra è molto sottile, cioè D≈0, le (3.41) e (3.45) perdono di significato e dalla (3.44) si ha
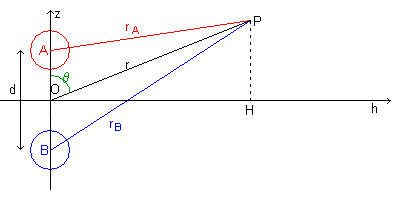
Si dice dipolo un sistema di due cariche di uguale intensità Q ma di segno opposto.
Con riferimento alla figura, si indica con
Assumendo come asse z di un sistema di riferimento cartesiano la retta AB e come piano xy il piano perpendicolare ad AB e passante per O del segmento AB, si ha
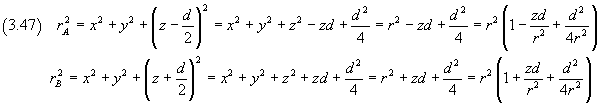
Se d è molto minore di r, con buona approssimazione si ha
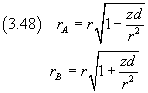
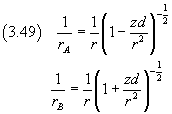
Lo sviluppo in serie della potenza di un binomio (1+x)α è
per x approssimativamente nullo si ha
quindi con buona approssimazione le (3.49) possono essere scritte
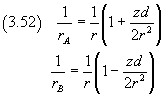
Per la (3.19) il potenziale in P risulta
Detto θ l'angolo AOP, si ha
e quindi
Detti ur il versore OP, k il versore dell'asse z e introducendo il vettore p, detto momento di dipolo, di intensità p=Qd e diretto dalla carica negativa a quella positiva,
la (3.54) può essere espressa nei seguenti modi
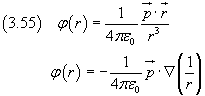
Riscrivendo la (3.53) nel seguente modo
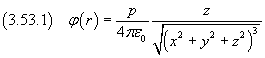
si possono calcolare le componenti cartesiane del campo elettrico, dato dall'opposto del gradiente del potenziale:
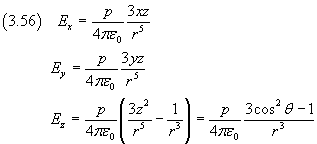
La componente del campo elettrico sul piano xy, detta componente trasversale, è
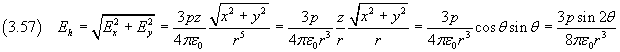
La (3.57) evidenzia che la componente trasversale è nulla per θ=0° e θ=90°, dove invece la componente assiale assume valori
