6. Onde e.m. nel vuoto

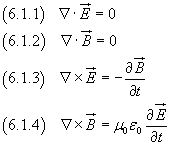
Nel vuoto, in assenza di cariche e correnti, indicando con ε₀ la permittività elettrica e con μ₀ la permeabilità magnetica, le equazioni di Maxwell (4.8) assumono la seguente forma:

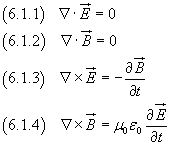
Uguagliando il rotore di entrambi i membri nella (6.1.3) si ha

e, ricavando il rotore di B dalla (6.1.4), si ha

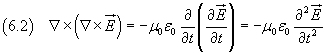
Dall'identità (5.10) inoltre si ha

e, per la (6.1.1),

Uguagliando i secondi membri nelle uguaglianze (6.2) e (6.3) si ottiene

Operando in modo analogo sull'equazione relativa al rotore di B, si ottiene anche

Se si pone e si rappresentano i campi con ψ si ottiene l'equazione di d'Alembert

che ammette soluzioni generali, dette funzioni d'onda, di tipo

Quindi, nel vuoto, campi elettrici e magnetici, si propagano come onde di velocità di modulo .

Ricavato dalle misure della permeabilità e della permittività del vuoto, il valore di questa velocità coincide con quelle della luce c, misurato otticamente da Foucault. Di conseguenza, le (6.4) e (6.5) possono più semplicemente essere scritte

Se, per semplicità, si assumono come soluzioni della (6.7) e (6.8) funzioni d'onda sferiche sinusoidali di pulsazione ω e numero d'onda k e si esprimono queste soluzioni in forma esponenziale complessa

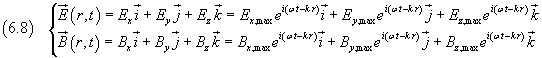
dove r > 0 rappresenta la distanza di un punto P da una sorgente puntiforme nell'origine O,

si ottiene

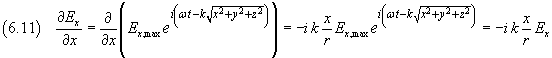
e analogamente, per le altre due componenti,

La divergenza di E risulta allora

Per la (6.1.1) la divergenza di E è nulla, dunque

La (6.15) implica che il vettore E è ortogonale al vettore r, cioè nelle onde elettromagnetiche nel vuoto, il campo elettrico è perpendicolare alla direzione di propagazione.

Dato che anche B ha divergenza nulla, la stessa conclusione vale anche per il campo di induzione magnetica.

Il rotore di E risulta

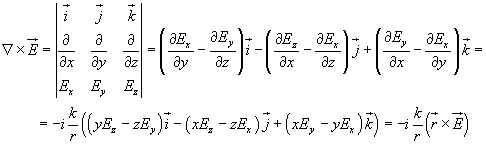
Per (6.1.3) si ha

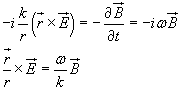
e in definitiva

dove u_r è il versore della direzione di propagazione. La (6.17) mostra che E e B, oltre ad essere perpendicolari alla direzione di propagazione r, sono perpendicolari tra loro formando una terna levogira. Inoltre, uguagliando i moduli dei due membri della (6.16) si ha

La sistemazione teorica dell'elettromagnetismo operata da Maxwell non è stata una pura riorganizzazione assiomatica delle conoscenze precedentemente acquisite, ma è stata una vera rivoluzione scientifica e tecnologica:

• ha previsto l'esistenza di onde e.m. molto prima che queste fossero rilevabili o producibili sperimentalmente; anzi, senza questa teoria non ci sarebbe stata ricerca sperimentale e tecnologica;
• ha prodotto una rifondazione di tutta l'ottica, imponendo la reinterpretazione dei fenomeni luminosi come fenomeni elettromagnetici;
• dato che queste equazioni sono incompatibili con la relatività galileiana, hanno reso necessaria una riformulazione del principio dei relatività con la proposizione della teoria della relatività ristretta da parte di Einstein.