, possono essere idealizzati come
costituiti da infiniti elementi infinitesimi di volume
d
ognuno dei quali contiene una massa infinitesima dm tali che per ognuno di essi può essere definita
la densità ρI comuni corpi fisici dotati di estensione, caratterizzati quindi oltre che dalla loro massa m anche dal loro
volume
, possono essere idealizzati come
costituiti da infiniti elementi infinitesimi di volume
d
ognuno dei quali contiene una massa infinitesima dm tali che per ognuno di essi può essere definita
la densità ρ
quindi
Se ρ è costante, cioè se il corpo è omogeneo,
Se la masserella dm, collocata nel punto O, interagisce con le masserelle contigue in modo che uno spostamento dalla sua posizione di equilibrio sia contrastato da una forza opposta allo spostamento e direttamente proporzionale ad esso, cioè da una forza elastica, la massa dm risponde ad un suo spostamento con un moto armonico. A sua volta lo spostamento di una massa dm, per effetto delle sue interazioni con le masserelle contigue, determina un loro spostamento dalla posizione di equilibrio e quindi anche queste masserelle cominceranno ad oscillare con moto armonico.
Questo è ciò che succede, ad esempio, quando un sasso colpisce un punto O sulla superficie immobile di uno stagno. Il punto O, spostato dalla sua posizione di equilibrio dall'impatto del sasso, dopo l'affondamento del sasso, è sottoposto a forze contrarie allo spostamento, dovute alla tensione superficiale e alla forze intermolecolari, e incomincia ad oscillare con moto armonico; dopo un po' di tempo, ogni altro punto P della superficie dello stagno oscillerà con moto armonico, come si può verificare osservando il moto di qualunque oggetto abbastanza piccolo che galleggi nello stagno.
Il fenomeno di oscillazione che investe tutti i punti della superficie dello stagno è detto onda sinusoidale.
Nell'esempio delle onde nello stagno, la superficie dello stagno è il mezzo di propagazione dell'onda. Gli insiemi dei punti contigui della superficie che oscillano in fase, cioè che in ogni istante hanno la stessa quota, sono circonferenze dette fronti d'onda. Il punto O, centro dei fronti d'onda, è detto sorgente dell'onda.
Il moto armonico di O è descritto, nell'esempio dello stagno, dall'andamento nel tempo della sua quota z rispetto alla superficie imperturbata dello stagno. Con una opportuna scelta dell'origine dei tempi, z varia nel tempo secondo la legge
dove A, l'ampiezza, rappresenta in questo caso il modulo dello scostamento massimo della quota zO dalla posizione di equilibrio.
Se si ammette che O possa mantenere nel tempo la sua ampiezza e che il mezzo sia perfettamente elastico, in qualunque altro punto P, posto a distanza r da O, dopo un certo tempo t, dipendente da r e dal modulo della velocità costante v di propagazione della perturbazione, la quota z di P comincerà ad oscillare con moto armonico, con ugual ampiezza e pulsazione, ma in ritardo rispetto a O, ritardo tanto maggiore quanto maggiore è la distanza da O e tanto minore quanto maggiore è la velocità di propagazione dell'onda.
z quindi varierà nel tempo con andamento espresso da
Ma in generale ciò che succede alla quota di un punto sulla superficie di uno stagno può verificarsi per altre grandezze, scalari o vettoriali, indicate di seguito con il simbolo Ψ, funzioni variabili nel tempo della posizione di un punto P di un mezzo continuo se P viene raggiunto da una perturbazione di queste grandezze generata da una sorgente O a distanza r da P e propagantesi con velocità costante v.
animazione
Nel caso in cui Ψ sia una grandezza scalare (come, ad sempio, la pressione) o vettoriale e parallela alla velocità di propagazione v l'onda si dice longitudinale.
animazione
Se invece la grandezza vettoriale Ψ è perpendicolare a v l'onda si dice trasversale.
animazione
Approfondimento: Effetto Doppler.
Nel caso di onde trasversali risulta spesso importante valutare l'angolo che piano contenente il vettore Ψ e la velocità v forma rispetto ad un piano di riferimento prefissato. Il piano che contiene tale angolo è detto piano di polarizzazione e può essere costante o ruotare durante la propagazione dell'onda.
Va infine osservato che la velocità di propagazione dipende solo dalle caratteristiche del mezzo ed è quindi assolutamente indipendente dalla sorgente. Ad esempio:
(T: tensione; μ:densità lineare)
(γ: rapporto cp/cv; p: pressione;
ρ: densità)
(B: modulo di compressione; ρ: densità)
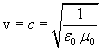(ε0: costante dielettrica;
μ0: permeabilità magnetica)
Il punto P sarà in generale un punto di un mezzo tridimensionale, quindi i fronti d'onda (supponendo il mezzo omogeneo e isotropo) saranno superfici sferiche.
Il comportamento della grandezza Ψ, in analogia con quello della quota z della (3.5), sarà espresso da
La (3.6) è detta equazione d'onda.
Sostituendo nella (3.6) l'espressione di ω della (2.10) si ottiene anche
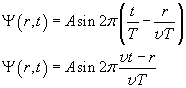
Il prodotto vT rappresenta lo spazio percorso da un fronte d'onda in un periodo T, detto lunghezza d'onda λ
Si ha quindi
La funzione d'onda Ψ può essere espressa in modo più conciso e significativo nel seguente modo
dove il coefficiente
è detto numero d'onda.
Dalle (3.7) e (3.9) si ottiene
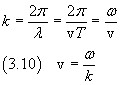
Dalla (3.8) la derivata seconda di Ψ rispetto al tempo risulta
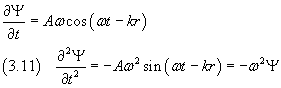
Nella (3.6) lo scalare r rappresenta la distanza di un punto P dalla sorgente O. Se P ha coordinate cartesiane x, y, z, si ha
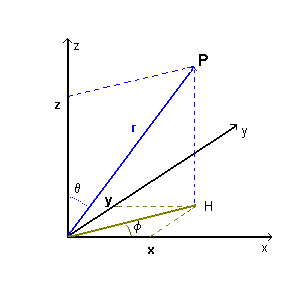
La derivata parziale prima di Ψ rispetto a x risulta
Dato che
con θ e φ costanti in quanto l'onda si propaga radialmente, si ha
La derivata seconda, sempre rispetto a x, risulta
In modo analogo si ottengono le derivate seconde di Ψ rispetto a y e z
Sommando membro a membro le (3.12), (3.13) e (3.14) si ottiene
Introducendo l'operatore differenziale
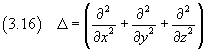
detto Laplaciano, la (3.15) può essere scritta
Confrontando le (3.11) e (3.17) si ottiene
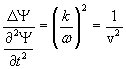
e infine
La (3.18) è nota come equazione di d'Alembert. Quindi una funzione d'onda sinusoidale soddisfa l'equazione di d'Alembert. Viceversa si assume che ogni funzione che soddisfa l'equazione di d'Alembert è una funzione d'onda.
Talora, per ottenere una espressione più sintetica dell'equazione di d'Alembert, si usa l'operatore
detto d'Alembertiano, e la (3.18) diventa semplicemente
Se si assume che nell'istante iniziale una funzione d'onda sinusoidale nel punto in cui si trova la sorgente abbia il suo valore massimo, allora la funzione è espressa da
Notando che l'espressione
, si può interpretare la (3.21)
come la parte reale della funzione complessa
nella descrizione delle onde si può usare direttamente la (3.22) ottenendo, in molte situazioni, vantaggi notevoli nella esposizione e nella elaborazione.
In particolare in un mezzo materiale unidimensionale un punto P di massa dm che oscilla armonicamente con ampiezza A e pulsazione ω, per la (2.13), ha energia totale
Considerando come volume infinitesimale
d
quello di un guscio sferico centrato sulla sorgente O, di raggio r e spessore dr
dalla (3.23) si ottiene
Dividendo entrambi i membri per dt
Il primo membro della (3.10) rappresenta la potenza che attraversa una superficie sferica di raggio r, cioè la quantità di energia che attraversa la superficie nell'unità di tempo.
Dividendo il secondo membro della (3.10) per la superficie del fronte d'onda sferico
, si ottiene
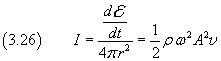
La grandezza I così ottenuta rappresenta la quantità di energia che investe l'unità di superficie nell'unità di tempo ed è detta intensità.
Introducendo la grandezza
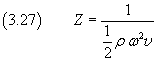
detta impedenza, l'intensità può essere espressa nel seguente modo
