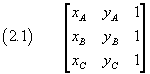
L'espressione tra parentesi nella (1.1) può essere più comodamente denotata ricorrendo all'uso di un determinante 3x3 (terzo ordine), cioè di una tabella composta da tre righe e tre colonne di numeri reali
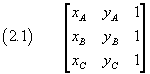
da sviluppare nel seguente modo, detto:
Regola di Laplace
Il valore di un determinante si ottiene sommando i prodotti tra ogni elemento di una riga o di una sua colonna per il suo complemento algebrico.
Il complemento algebrico di un elemento aij (i: indice di riga; j: indice di colonna)
è il determinante che risulta cancellando la riga i-esima e la colonna j-esima
moltiplicato per (-1)i+j,
cioè per 1 se i+j è pari, per -1 se i+j è dispari.
Come si vede la regola di Laplace è ricorsiva, cioè per calcolare un determinante di ordine n bisogna calcolare n determinanti di ordine n-1. Il processo termina quando i complementi algebrici sono 'determinanti di ordine 1', vale a dire i singoli elementi del determinante stesso.
Ad esempio, il determinante scritto sopra si può sviluppare nel seguente modo secondo gli elementi della prima riga:
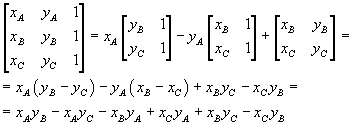
Può essere un utile esercizio verificare che si ottiene lo stesso risultato sviluppando il determinante secondo gli elementi di un'altra riga o di un'altra colonna.
Si può quindi concludere che l'area del triangolo ABC considerato risulta esprimibile nel seguente modo
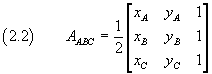
La relazione (2.2) è stata ottenuta considerando un particolare triangolo (acutangolo, con i vertici in determinati quadranti, ecc..), ma si può facilmente verificare ragionando in modo analogo su altre disposizioni che il risultato è generalizzabile se si ha l'avvertenza di ordinare i vertici (e quindi le righe del determinante (2.1) ) in senso antiorario.
Infatti una notevole proprietà dei determinanti è la seguente:
se in un determinante si scambiano tra di loro due righe (o due colonne) il determinante cambia di segno.
Si provi a sviluppare il seguente determinante
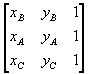
ottenuto dal determinante (2.1) scambiando tra di loro la prima e la seconda riga.
Dal punto di vista geometrico l'inversione delle due righe corrisponde ad un orientamento orario dei vertici.
Si può dunque affermare che
Se i vertici sono ordinati in senso antiorario l'area risulta positiva; se invece i vertici sono ordinati in senso orario l'area risulta di uguale valore assoluto ma di segno negativo.
Poiché in geometria euclidea si prescinde dall'ordinamento lineare e rotazionale dei punti e le lunghezze dei segmenti e le aree delle figure sono considerate solo in modulo, si può dire che l'area euclidea di un triangolo di vertici ABC è
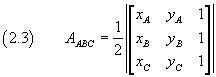
Se si conoscono i fondamenti del calcolo vettoriale, l'area del triangolo in funzione delle coordinate dei vertici può essere dedotta molto più direttamente.