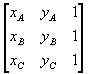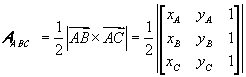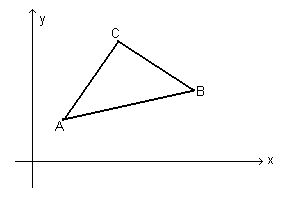
Chi conosca i fondamenti del calcolo vettoriale può agevolmente dedurre l'espressione dell'area di un triangolo date le coordinate dei vertici, ricordando che il modulo del prodotto vettoriale può essere interpretato geometricamente come l'area del parallelogramma che si ottiene applicando le rappresentazioni sagittali dei due vettori allo stesso punto e e tracciando per le punte dei vettori le parallele ai vettori stessi.
Si può quindi concludere che l'area del triangolo individuato da due vettori coincide con la metà del modulo del loro prodotto vettoriale.
Dato nel piano cartesiano ortogonale Oxy il triangolo ABC
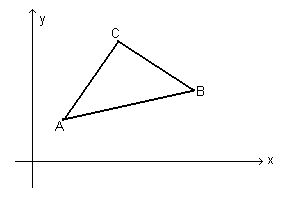
i lati AB e BC possono essere interpretati come vettori
![]()
![]()
Il loro prodotto vettoriale è
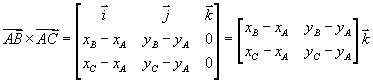
Sviluppando il determinante
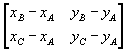
si vede che esso è del tutto equivalente al determinante