Un sistema lineare del tipo
![]()
può essere interpretato nel seguente modo
![]()
Si tratta cioè di determinare, se è possibile, un vettore v(x;y) tale che,
applicando ad esso l’operatore S di matrice
![]() ,
si ottenga il vettore v’(c;c’) o, più sinteticamente,
di risolvere l'equazione
,
si ottenga il vettore v’(c;c’) o, più sinteticamente,
di risolvere l'equazione
![]()
Dall'algebra elementare si ottiene
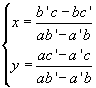
Condizione necessaria perché il sistema abbia una soluzione determinata è che l'espressione che compare a denominatore delle due frazioni a secondo membro non sia nulla. Tale espressione formata solo dagli elementi della matrice di S è detta determinante di S.
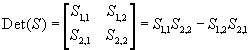
N.B.: In questa esposizione, per chiarezza didattica e grafica, si denotano le matrici inserendo i loro elementi tra parentesi tonde e i loro determinanti inserendo gli elementi tra parentesi quadrate.
Indicando con Δ il determinante di S, se tale determinante non è nullo, si può scrivere
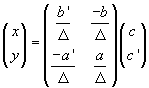
Indicando con S-1 l’operatore la cui matrice appare a secondo membro si può sinteticamente scrivere che la soluzione dell'equazione
![]()
è data da
![]()
La matrice S-1 moltiplicata per S da come risultato la matrice Identità. Si può quindi dire che S-1 è la matrice reciproca (o inversa) di S.
La matrice reciproca di S esiste solo se il determinante di S non è nullo.
Quindi condizione necessaria perché una matrice sia invertibile è che il suo determinante non sia nullo.
Una matrice quadrata bidimensionale invertibile individua una trasformazione lineare biunivoca tra i vettori di ℜ2
In generale, per calcolare la matrice inversa di una matrice si può seguire questa procedura.
Si calcola il determinante della matrice. Per matrici quadrate di ordine superiore a 2 si può usare la regola di Laplace
.Per complemento algebrico di un elemento Li,jdi una matrice si intende il determinante che si ottiene eliminando nella matrice data la riga i e la colonna j moltiplicato per (-1)i+j.
In seguito, parlando di trasformazioni lineari, si intenderà sempre una trasformazione lineare invertibile.
Esempi.
Data la matrice
![]()
si ha Δ=2 e la matrice inversa risulta
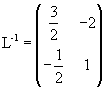
Moltiplicando la matrice L per la sua inversa L-1 si ha
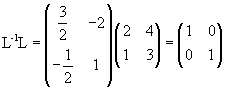
Il sistema
![]()
può essere rappresentato dall'equazione matriciale
![]()
La soluzione di questa equazione è
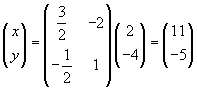
Questo metodo può essere esteso a sistemi di grado superiore. Ovviamente all'aumentare del grado del sistema la mole di calcolo aumenta notevolmente, per cui è utile ricorrere a strumenti di calcolo automatico come, ad esempio un foglio elettronico o software specializzato come Mathematica (©Wolfram). In questo sito è disponibile l'applicazione Supercalcolatrice.