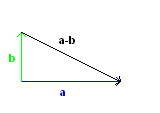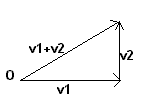
Riprendendo l'esempio proposto nel paragrafo precedente, se un'auto, muovendosi da un certo punto, si sposta di 4 Km verso E e poi si sposta di 3 Km verso N, si sposta di 5 Km rispetto al punto di partenza ma la direzione dello spostamento è intermedia tra E e N.

Definendo come risultante o somma di due successivi spostamenti lo spostamento complessivo dal punto iniziale O, è evidente che tale somma non è data dalla somma aritmetica delle lunghezze dei singoli spostamenti, ma è rappresentata da un vettore con un estremo nella coda del primo e la punta nella punta del secondo.

Allo stesso risultato si giunge se applicando entrambi i vettori di spostamento allo stesso punto O, si definisce come loro somma la diagonale del parallelogramma di cui i vettori costituiscono due lati consecutivi.

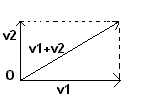
In generale la somma di due vettori si effettua nello stesso modo della composizione degli spostamenti.

È abbastanza immediato verificare che la somma di due vettori è indipendente dall'ordine degli addendi: essa è quindi commutativa.

Due vettori di uguale intensità e direzione ma verso opposto hanno come risultante un vettore di lunghezza nulla, per il quale è impossibile stabilire direzione e verso. Per regolarità formale si può continuare a qualificare tale risultante come vettore, denominandola vettore nullo.

Il vettore nullo sommato a qualunque altro vettore ha come risultante il vettore sommato. Per questo motivo è detto elemento neutro della somma.

Due vettori con risultante nulla si dicono opposti.

Se si considerano tre vettori e si aggiunge il terzo alla somma dei primi due oppure si aggiunge il primo alla somma degli ultimi due il risultato non cambia: la somma di vettori è associativa.

Un insieme su cui è definita una operazione interna (componendo due elementi si ottiene uno e un solo elemento dello stesso insieme) è detto struttura algebrica. Se l'operazione è associativa, ammette un elemento neutro e l'opposto per ogni elemento, tale struttura è detta gruppo. L'insieme dei vettori geometrici con l'operazione di somma sopra definita è un gruppo commutativo.

In un gruppo si può definire l'operazione inversa: la differenza tra due vettori è data dalla somma del primo vettore con l'opposto del secondo.

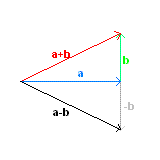
Per l'equivalenza dei vettori traslati, il vettore differenza può essere ottenuto entrambi i vettori ad O e tracciando un vettore dalla punta del sottraendo alla alla punta del minuendo.