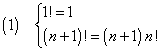
(edited by Roberto Bigoni)
The factorial n! of a natural number n>0 is recursively defined by
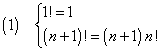
L. Euler extended this recursion property also to real and complex numbers by defining a function, now said Γ (Gamma), such that
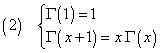
Indeed, if we apply this function to an argument x+1 coincident with a natural number, we have
Euler could explicitly express the Γ in this way:
In fact, from this definition we have
and also
So this definition verify the equations in (2) and is a valid expression of Γ.
Conversely, for natural arguments n, we can write
Other interesting values of Γ can be seen in Euler's integrals.
If we let
in the integral in (7), we get
and after
By multiplying and dividing the integrand by en and extracting from the integral the factors which don't depend on integration variable y, we have
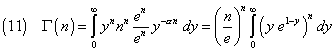
The derivative of the integrand
is 
so f(y) has an absolute maximum for y=1.
To approximate the integral it is convenient to express it as a function of w=y-1
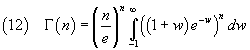
and, after, to approximate the integrand f(w) in the following way (see mathworld):
We calculate the logarithm of the function:
If n is big enough, the function rapidly converge to 0 to the left and to the right of the maximizing value, so we can assume that the absolute value of w is very close to 0 and expand the logarithm in this way:
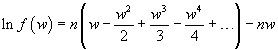
that is
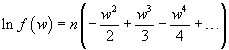
The absolute value of w is very small, so we can truncate the expansion to the first term
that is
Now, from (12), we have
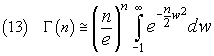
Remembering that the function f(w) is very close to 0 in a neighborhood of 1, we can take the integral from -∞ to a +∞ without sensible loss of precision
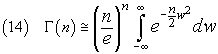
The integral in (14) is a
gaussian integral
and its value is
;
therefore we have
At the end we get
The (15) is the Stirling's approximation for n!, very useful in a large number of probabilistic and statistical calculations.
For example, using (15):
To get an approximation of the logarithm of a factorial, from (15) we have
The second addend, when n is big, may be disregarded and it is sufficient to assume
