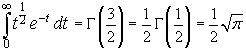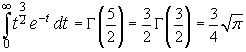(notes by Roberto Bigoni)
The integrals that express the Euler's Gamma function
![]()
are such that
![]()
![]()
In particular, if x is a natural number greater than 1, we have
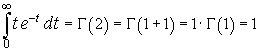
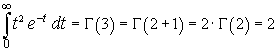
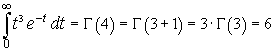
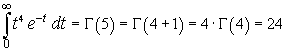
In general
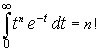
To calculate the value of Gamma when its argument is an half-integral number, we must first calculate
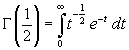
Using the variable substitution t=z2 we get
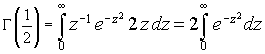
This integral is a
gaussian integral
and its value is
![]() .
So
.
So
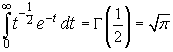
The values of Gamma for the following half-integral arguments can be obtained recursively