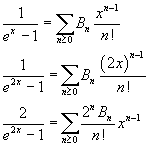
From the results obtained in the previous section we can easily deduce
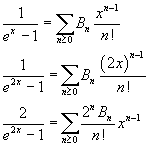
Using the (3.9) to express the hyperbolic cotangent, we have
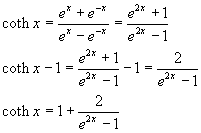
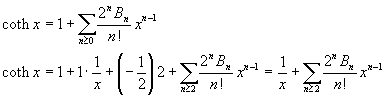
If we explicitly write some addends of the sum we have
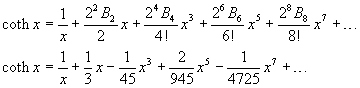
Finally, using a more formal and compact notation:
![]()
The series expansion of the circular cotangent can be obtained from the (9.1), (7.21) and (7.22)
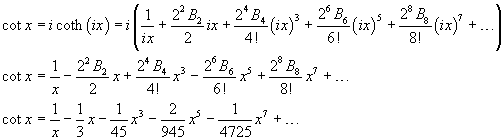
In a more compact way:
![]()
To deduce the series expansion of the hyperbolic tangent we can use the equality
![]()
In fact
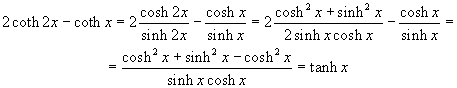
So, using twice the series expansion of the hyperbolic cotangent, we get
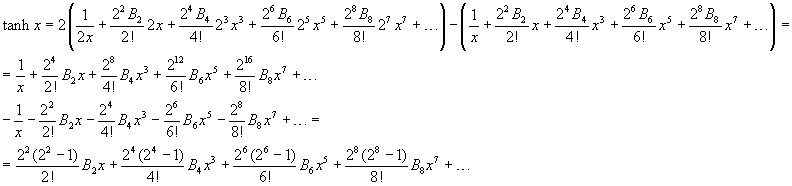
If we calculate explicitly the coefficients, we have
![]()
In a more compact way:
![]()
To have the series expansion of the circular tangent we use the equality
![]()
We get
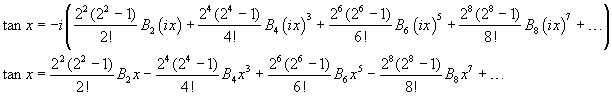
If we calculate explicitly the coefficients, we have
![]()
In a more compact way:
![]()
Since
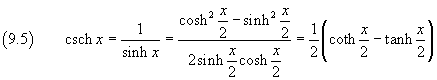
the series expansion of the hyperbolic cosecant can be obtained using the series expansions of the hyperbolic tangent and cotangent. From (9.1) and (9.3) we get
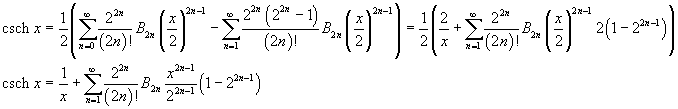
![]()
More explicitly
![]()
From (7.22) e (9.7) we get
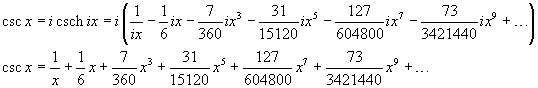
and, in more compact way
![]()
The hyperbolic secant can be expressed as a function of the exponential
![]()
This expression of the hyperbolic secant coincides with that of the function s(x) defined in (8.2) of the previous page, then
![]()
where En is the n-th Euler's number. Since, for odd indices these numbers are zero, we can more economically write
![]()
From the Euler's formulas, the circular secant can be expressed as
![]()
The even powers of the imaginary unit oscillate between 1 and -1, then
![]()