Ministero dell'Istruzione, dell'Università e della Ricerca
ESAME DI STATO DI ISTRUZIONE SECONDARIA SUPERIORE
Indirizzi: LI02, EA02 - SCIENTIFICO
LI03 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE
LI15 - SCIENTIFICO - SEZIONE AD INDIRIZZO SPORTIVO

(Testo valevole anche per le corrispondenti sperimentazioni internazionali e quadriennali)

Tema di: MATEMATICA e FISICA

Il candidato risolva uno dei due problemi e risponda a 4 quesiti.

PROBLEMA 1

Si considerino le seguenti funzioni:

• Provare che, comunque siano scelti i valori di a e b in ℝ con a≠0, la funzione g ammette un massimo e un minimo assoluti. Determinare i valori di a e b in corrispondenza dei quali i grafici delle due funzioni f e g si intersecano nel punto .
• Si assuma, d'ora in avanti, di avere a = 1 e b = -1. Studiare le due funzioni così ottenute, verificando che il grafico di g ammette un centro di simmetria e che i grafici di f e g sono tangenti nel punto . Determinare inoltre l'area della regione piana S delimitata dai grafici delle funzioni f e g.

•  

  Si supponga che nel riferimento Oxy le lunghezze siano espresse in metri (m). Si considerino tre fili conduttori rettilinei disposti perpendicolarmente al piano Oxy e passanti rispettivamente per i punti: 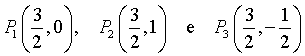. I tre fili sono percorsi da correnti continue di intensità i1 = 2,0 A, i2 e i3. Il verso di i1 è indicato in figura mentre gli altri due versi non sono indicati. Stabilire come varia la circuitazione del campo magnetico, generato dalle correnti i1, i2 e i3, lungo il contorno di S, a seconda dell'intensità e del verso di i2 e i3.

• Si supponga, in assenza dei tre fili, che il contorno della regione S rappresenti il profilo di una spira conduttrice di resistenza R = 0,20 Ω.
  La spira è posta all'interno di un campo magnetico uniforme di intensità perpendicolare alla regione S.
  Facendo ruotare la spira intorno all'asse x con velocità angolare ω costante, in essa si genera una corrente indotta la cui intensità massima è pari a 5,0 mA.
  Determinare il valore di ω.

svolgimento

PROBLEMA 2

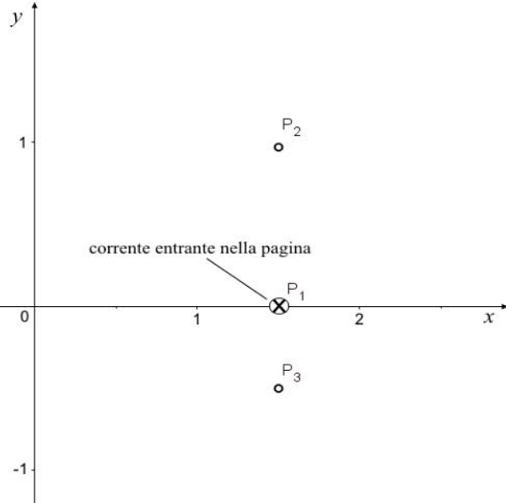
Un condensatore piano è formato da due armature circolari di raggio R, poste a distanza d, dove R e d sono espresse in metri (m).
Viene applicata alle armature una differenza di potenziale variabile nel tempo e inizialmente nulla.

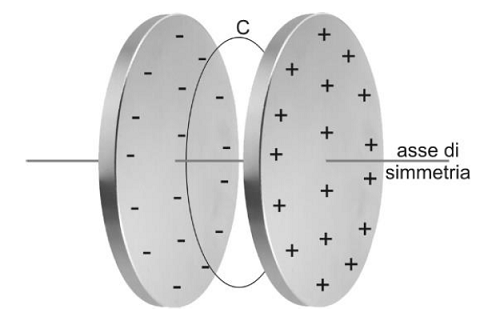
All'interno del condensatore si rileva la presenza di un campo magnetico .
Trascurando gli effetti di bordo, a distanza r dall'asse di simmetria del condensatore, l'intensità di , espressa in tesla (T), varia secondo la legge

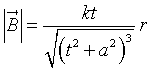
dove a e k sono costanti positive e t è il tempo trascorso dall'istante iniziale, espresso in secondi (s).

• Dopo aver determinato le unità di misura di a e k, spiegare perché nel condensatore è presente un campo magnetico anche in assenza di magneti e correnti di conduzione.
  Qual è la relazione tra le direzioni di e del campo elettrico nei punti interni al condensatore?

• Si consideri, tra le armature, un piano perpendicolare all'asse di simmetria. Su tale piano, sia C la circonferenza avente centro sull'asse e raggio r.
  Determinare la circuitazione di lungo C e da essa ricavare che il flusso di , attraverso la superficie circolare delimitata da C, è dato da
  

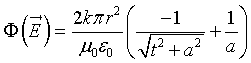
  Calcolare la d.d.p. tra le armature del condensatore.

  A quale valore tende al trascorrere del tempo? Giustificare la risposta dal punto di vista fisico.

• Per a > 0, si consideri la funzione definita da
  .
  Verificare che la funzione
  
  è la primitiva di f il cui grafico passa per l'origine.
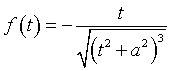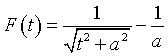
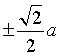  Studiare la funzione F, individuandone eventuali simmetrie, asintoti, estremi. Provare che f presenta due flessi nei punti di ascisse e determinare le pendenze delle rette tangenti al grafico di F in tali punti.
• Con le opportune motivazioni, dedurre il grafico di f da quello di F, specificando cosa rappresentano le ascisse dei punti di flesso di F per la funzione f.
  Calcolare l'area della regione compresa tra il grafico di f, l'asse delle ascisse e le rette parallele all'asse delle ordinate passanti per gli estremi della funzione.
  Fissato b > 0, calcolare il valore di .

svolgimento

QUESTIONARIO

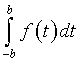1. Una data funzione è esprimibile nella forma 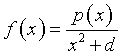, dove d ∈ ℝ e p(x) è un polinomio.
   Il grafico di f interseca l'asse x nei punti di ascisse 0 e 12/5 ed ha come asintoti le rette di equazione x = 3, x = -3 e y = 5.
   Determinare i punti di massimo e di minimo relativi della funzione f.

   svolgimento

2. È assegnata la funzione

   

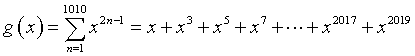
   Provare che esiste un solo x₀ ∈ ℝ tale che g(x₀) = 0. Determinare inoltre il valore di

   

   svolgimento

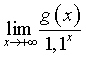
3. Tra tutti i parallelepipedi rettangoli a base quadrata, con superficie totale di area S, determinare quello per cui la somma delle lunghezze degli spigoli è minima.

   svolgimento

4. Dati i punti A(2,0,-1) e B(-2,2,1), provare che il luogo geometrico dei punti P dello spazio, tali che , è costituito da una superficie sferica S e scrivere la sua equazione cartesiana.
   Verificare che il punto T(-10,8,7) appartiene a S e determinare l'equazione del piano tangente in T a S.

   svolgimento

5. Si lanciano 4 dadi con facce numerate da 1 a 6.

   • Qual è la probabilità che la somma dei 4 numeri usciti non superi 5?
   • Qual è la probabilità che il prodotto dei 4 numeri usciti sia multiplo di 3?
   • Qual è la probabilità che il massimo numero uscito sia 4?

   svolgimento

6.  

   Una spira di rame, di resistenza R = 4,0 mΩ, racchiude un'area di 30 cm2 ed è immersa in un campo magnetico uniforme, le cui linee di forza sono perpendicolari alla superficie della spira. La componente del campo magnetico perpendicolare alla superficie varia nel tempo come indicato in figura. Spiegare la relazione esistente tra la variazione del campo che induce la corrente e il verso della corrente indotta. Calcolare la corrente media che passa nella spira durante i seguenti intervalli di tempo: a) da 0,0 ms a 3,0 ms; b) da 3,0 ms a 5,0 ms; c) da 5,0 ms a 10 ms.

   svolgimento

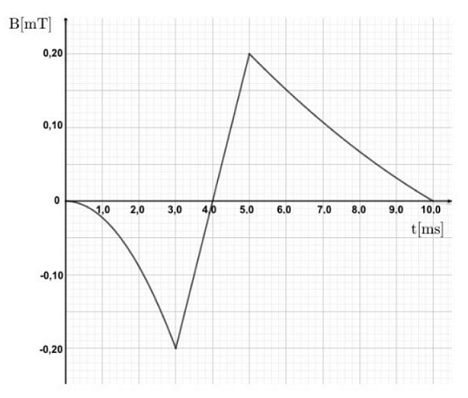7. In laboratorio si sta osservando il moto di una particella che si muove nel verso positivo dell'asse x di un sistema di riferimento ad esso solidale.
   All'istante iniziale, la particella si trova nell'origine e in un intervallo di tempo di 2,0 ns percorre una distanza di 25 cm.
   Una navicella passa con velocità v = 0,80c lungo la direzione x del laboratorio, nel verso positivo, e da essa si osserva il moto della stessa particella.
   Determinare le velocità medie della particella nei due sistemi di riferimento. Quale intervallo di tempo e quale distanza misurerebbe un osservatore posto sulla navicella?

   svolgimento

8. Un protone penetra in una regione di spazio in cui è presente un campo magnetico uniforme di modulo = 1,00 mT.
   Esso inizia a muoversi descrivendo una traiettoria ad elica cilindrica, con passo costante Δx = 38,1 cm, ottenuta dalla composizione di un moto circolare uniforme di raggio r = 10,5 cm e di un moto rettilineo uniforme. Determinare il modulo del vettore velocità e l'angolo che esso forma con .

   svolgimento

_______________________________________________________________

Durata massima della prova: 6 ore.
È consentito l'uso di calcolatrici scientifiche e/o grafiche purché non siano dotate di capacità di calcolo simbolico (O.M. n. 257 Art. 18 comma 8).
È consentito l'uso del dizionario bilingue (italiano-lingua del paese di provenienza) per i candidati di madrelingua non italiana.
Non è consentito lasciare l'Istituto prima che siano trascorse 3 ore dalla dettatura del tema.