Questionario - 2007

Quesito 1

Nella geometria greca classica, il problema di quadrare il cerchio consisteva nella ricerca di una costruzione con riga e compasso di un segmento di lunghezza equivalente alla circonferenza di diametro assegnato o di una costruzione equivalente. Il problema, come altri classici analoghi problemi (la trisezione dell'angolo, la duplicazione del cubo) si è dimostrato insolubile, in quanto π è un numero irrazionale trascendente.

Quesito 2

Ognuno delle sezioni rettangolari può essere concepita come un parallelepipedo di superficie di base e spessore dx il cui volume è quindi . Il volume totale del solido risulta dalla somma di questi volumi infinitesimi:

Ponendo si ha

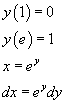
e quindi

Calcolando per parti l'integrale indefinito, si ha

L'integrale definito vale quindi

In definitiva

Quesito 3

Limitandosi alla considerazione di spazi vettoriali bidimensionali, scegliendo un sistema di riferimento con origine in O, le omotetie sono trasformazioni lineari di matrice

Alla composizione di due omotetie H e K corrisponde la matrice prodotto

che è pure un'omotetia: quindi la composizione è un'operazione interna commutativa.

L'identità, rappresentata dalla matrice

è essa stessa un'omotetia, quindi la composizione di due omotetie ammette un elemento neutro.

Per ogni omotetia H è definita l'omotetia H^-1

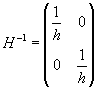
che composta con H produce l'elemento neutro. Dunque le omotetie sono invertibili.

Infine, date tre omotetie,

si ha che

quindi la composizione di omotetie è associativa.

Si può quindi concludere che l'insieme delle omotetie di ugual centro con l'operazione di composizione rappresentata dal prodotto delle loro matrici forma un gruppo commutativo (o abeliano).

Quesito 4

La funzione proposta rappresenta la densità di probabilità di una distribuzione gaussiana di valor medio μ e deviazione standard σ. σ² è lo scarto quadratico medio o varianza.

Il diagramma della funzione è la nota curva a campana di Gauss, che ha un massimo assoluto per x=μ, è simmetrica rispetto alla retta x=μ, ha flessi per x=μ ± σ è tende a 0 per valori molto distante dal valor medio.

L'integrale da x₁ a x₂ di questa funzione rappresenta la probabilità che una variabile casuale continua assuma valori compresi nell'intervallo [x₁ ; x₂].

Le distribuzioni gaussiane dei valori delle variabili hanno una notevole importanza, ad esempio, nella valutazione delle misure sperimentali delle grandezze fisiche, i cui valori sono rappresentati normalmente associando alla media delle rilevazioni della misura un'incertezza uguale al triplo della deviazione standard, in quanto in questo modo si individua un intervallo in cui è compresa la quasi totalità delle misure.

Quesito 5

Il teorema citato vale solo se si assume il cosiddetto quinto postulato di Euclide, cioè se si ammette che dati nel piano una retta e un punto esterno ad essa, per il punto passa una e una sola parallela alla retta data. Sostituendo a questo postulato affermazioni alternative, si possono costruire sistemi coerenti di proposizioni geometriche detti geometrie non-euclidee come quelle proposte da Gauss, Lobachevsky e Riemann. Queste geometrie sono dette iperboliche se ammettono l'esistenza di infinite parallele, ellittiche se non ammettono parallele.

Ad esempio, un modello intuitivo della geometria ellittica di Riemann può essere rappresentato considerando come 'piano' una superficie sferica e come 'rette' le circonferenze di diametro uguale a quello della sfera. Ipotizzando un globo terrestre perfettamente sferico, tutti i meridiani e l'equatore sarebbero 'rette'. Si comprende facilmente che il 'triangolo' formato da due meridiani e l'equatore è tale da avere la somma degli angoli interni maggiore di un angolo piatto, in quanto gli angoli che i meridiani formano con l'equatore sono entrambi retti e alla loro somma va aggiunto l'angolo formato dai meridiani nel polo in cui si incontrano.

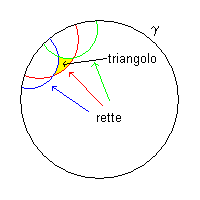
Come modello intuitivo di geometria iperbolica si può citare il modello di Poincaré, in cui si considera come 'piano' la superficie di un cerchio Γ delimitato dalla circonferenza γ e 'rette' gli archi di circonferenza interni a Γ, con estremi su γ con tangenti negli estremi coincidenti con raggi di γ. In questo modello si vede che nei 'triangoli' la somma degli angoli interni è minore di un angolo piatto.

Quesito 6

L'intersezione di un cerchio con centro in un vertice del triangolo e raggio unitario con il triangolo è 1/6 dell'area del cerchio, cioè . Assumendo come misura della probabilità che un punto abbia distanza da un vertice minore di 1 il rapporto tra l'area totale delle tre intersezioni e quella del triangolo, tale misura risulta

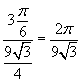
La probabilità chiesta è complementare a quella calcolata, cioè

Quesito 7

Il luogo richiesto è rappresentato geometricamente dalla perpendicolare alla tangente alla parabola nel punto P(1;2). Il coefficiente angolare di tale retta è dato dall'antireciproco del valore della derivata della funzione nel punto P.

L'equazione del luogo risulta dunque

Quesito 8

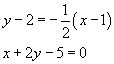
Indicando con x, y, z le somme iniziali possedute dai giocatori X, Y e Z, dopo la prima partita i giocatori possiedono

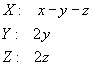
Dopo la seconda

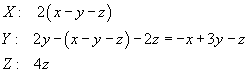
Dopo la terza

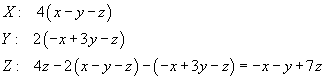
Le somme finali valgono tutte 24, quindi

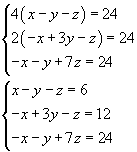
Il sistema ha soluzione

Quesito 9

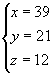
L'equazione proposta può essere interpretata come la risolvente del sistema

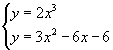
La prima equazione è rappresentata graficamente da una cubica sempre crescente con un flesso orizzontale nell'origine. La seconda da una parabola con asse parallelo all'asse delle ordinate, concavità verso l'alto, vertice in V(1;-9) e che interseca l'asse delle ascisse nei punti di ascissa .

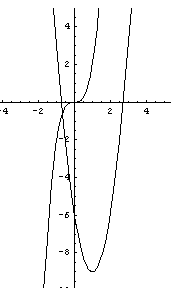
Le soluzioni dell'equazione proposta sono rappresentate graficamente dalle ascisse delle intersezioni delle due curve. Si osserva un'unica intersezione compresa tra -1 e 0. Calcolando i valori della funzione f(x) azzerata agli estremi di questo intervallo si ottiene f(-1)=-5 e f(0)=6 e poiché la funzione è continua, esiste sicuramente uno zero in tale intervallo.

Per approssimare tale zero si può usare il metodo delle tangenti, assumendo come primo termine della successione z₀=-1.

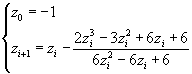
Si ottiene

Quesito 10

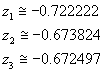
Detti poli i punti di intersezione dell'asse con la sfera, i meridiani sono, sulla superficie sferica, le semicirconferenze di diametro massimo passanti per i poli. I paralleli sono le circonferenze intersecate sulla sfera da piani perpendicolari all'asse. Il parallelo di lunghezza massima è detto equatore. Fissato un meridiano di riferimento γ (usualmente quello di Greenwich), il valore assoluto della longitudine di un punto P sulla sfera è la misura del diedro formato dai semipiani di γ e del meridiano passante per P; la longitudine si considera positiva se il P è a ovest di γ, negativa in caso contrario. Data la circonferenza α del meridiano per P, la latitudine di P è, in valore assoluto, la misura dell'angolo al centro di α i cui lati passano per P e per il punto di intersezione tra il meridiano per P e l'equatore. La latitudine si considera positiva se P è a nord dell'equatore, negativa in caso contrario. Usualmente longitudine e latitudine si misurano in gradi sessagesimali: la longitudine varia quindi da -180° a +180°, la latitudine da -90° a +90°. I sistemi satellitari (ad es. il GPS) e i servizi informatici (come Google Maps) usano di regola i gradi decimali.