Le funzioni circolari e iperboliche, esponenziali e logaritmiche o le costanti reali π e e, non sarebbero molto utili se non se ne potessero calcolare i valori.
Deve essere comunque chiaro che, dato che si tratta di valori reali, diversamente dal caso dei numeri razionali, in generale non è possibile esprimere questi valori completamente, qualunque sia la base di rappresentazione numerica adottata (base dieci, base due, sedici o altre). In generale, calcolare un numero reale α significa trovare un algoritmo che genera una successione di numeri razionali ai convergente a α. Quanto più cresce l'indice i, tanto più diminuisce la differenza tra l'ultimo ai e il precedente. Nelle applicazioni pratiche è sufficiente spingere il processo fino al punto in cui il calcolo di un successivo ai non produce vantaggi apprezzabili.
Probabilmente l'esempio più semplice ed immediato di una successione di questo tipo è la successione delle potenze con esponente
naturale crescente i di un numero razionale x compreso tra -1 e +1.
Quanto più i cresce, tanto più i termini xi=xi di questa successione si avvicinano a 0.
Si può esprimere formalmente questo fatto dicendo che per qualunque numero razionale x,
tale che |x|<1, per
quanto piccolo si scelga un numero razionale positivo ε, si può trovare un esponente
naturale positivo nε tale che, per ogni n maggiore di esso,
![]() .
.
Lo stesso concetto è espresso più immediatamente dalla seguente scrittura
![]()
che si legge: il limite di xn, per n tendente a infinito, è 0.
Esempio.
Sia x = 0.5. La successione delle sue potenze naturali con esponente crescente è
x0 = 0.50 = 1
x1 = 0.51 = 0.5
x2 = 0.52 = 0.25
x3 = 0.53 = 0.125
x4 = 0.54 = 0.0625
x5 = 0.55 = 0.03125
x6 = 0.56 = 0.015625
x7 = 0.57 = 0.0078125
x8 = 0.58 = 0.00390625
x9 = 0.59 = 0.001953125
...
Se si pone ε=0.01, si vede che, a partire da nε=7, tutti i termini xn successivi hanno valore assoluto minore di ε.
Se si considerasse un ε minore di 0.01, ad esempio 0.005, l'indice nε sarebbe 8, ma sarebbe sempre vero che tutti i termini xn successivi hanno valore assoluto minore di ε.
Questo esempio può essere un buon punto di partenza per trovare altre utili successioni convergenti ai numeri reali generati dalle funzioni trascendenti.
Si può facilmente verificare che, per ogni numero reale x diverso da 1,
![]()
e che
![]()
La somma in (7.2) è detta serie geometrica perché la successione dei suoi addendi è una successione geometrica, cioè il rapporto tra ogni termine della successione e il precedente è costante.
Il limite per n→∞ della serie è uguale al limite della frazione:
![]()
Se |x|<1, usando una notazione semplificata,
![]()
Dalla (7.3) si ha inoltre
![]()
Serie geometrica con WolframAlpha.
La frazione
![]() è la derivata rispetto a x di ln(1+x).
è la derivata rispetto a x di ln(1+x).
Quindi, per |x|<1 e ricordando che ln1=0,
si può viceversa dire che ln(1+x) è l'antiderivata della somma
![]() da cui
da cui
![]()
![]()
La (7.5) mostra che è possibile approssimare il logaritmo naturale nell'intervallo ]0;2[ e l'approssimazione sarà tanto migliore quanto più si aumenta il numero degli addendi della somma.
La somma (7.5) è detta serie di Mercatore. Questa serie ha un dominio di convergenza limitato e converge piuttosto lentamente, ma da essa si possono ricavare altre serie convergenti su tutto il dominio del logaritmo.
Infatti, dalla (7.5) si ottiene
![]()
Sottraendo membro a membro la (7.6) dalla (7.5) e ricordando le proprietà fondamentali dei logaritmi si ha
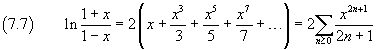
Dalla (7.7) si ha
![]()
Il primo membro della (7.8) è identico alla arcotangente iperbolica, quindi
![]()
Dalla (7.4) si ha
![]()
Integrando entrambi i membri e ricordando che arctan(0)=0, si ha
![]()
Dalla (7.10), ricordando che
![]() , si ottiene un algoritmo per approssimare π
, si ottiene un algoritmo per approssimare π
![]()
Questo metodo per approssimare π è conosciuto come serie di Leibniz.
Sviluppi in serie di arcotangenti con WolframAlpha.
Se si esamina la serie di Mercatore (7.5), si vede che i coefficienti cn
delle potenze xn nella somma sono tali che
![]() ,
dove f(n)(0) rappresenta il valore della derivata n-esima della funzione per x=0
e n! è il fattoriale dell'indice n. Per poter applicare questa espressione di cn
anche quando n=0, si assume che f(0)(x) è la funzione medesima e che 0!=1.
,
dove f(n)(0) rappresenta il valore della derivata n-esima della funzione per x=0
e n! è il fattoriale dell'indice n. Per poter applicare questa espressione di cn
anche quando n=0, si assume che f(0)(x) è la funzione medesima e che 0!=1.
Si potrebbe verificare che la stessa cosa vale per le funzioni arcotangente iperbolica e circolare (7.9) and (7.10) e, in generale, per qualunque altra funzione f(x) derivabile infinite volte, se la funzione e le sue derivate sono calcolabili per x=0. Infatti, da
![]()
si ottiene
In definitiva, per ogni funzione f(x) derivabile infinite volte, se la funzione e le sue derivate sono definite per x=0, si ha
![]()
La (7.13) è detta sviluppo in serie di MacLaurin
Il più immediato sviluppo in serie che si può ottenere usando la (7.13) è quello della esponenziale naturale ex per la quale tutte le derivate coincidono con la funzione stessa che per x=0 ha valore 1.
![]()
La serie (7.14) permette di approssimare il numero e=e1
![]()
Dalla (7.14) si ha inoltre
![]()
Dalle (7.14), (7.16) e (3.9), si ottengono le serie per il coseno e seno iperbolici che potrebbero comunque essere ricavate direttamente dalla (7.13)
![]()
![]()
Sviluppi in serie dell'esponenziale e del seno e coseno iperbolici con WolframAlpha.
Dalla (7.13) si possono agevolmente dedurre gli sviluppi in serie per i coseno e seno circolari
![]()
![]()
Se si usa la (7.17) per sviluppare coshix, dove i è l'unità immaginaria, si ottiene
![]()
![]()
Se si usa la (7.18) per sviluppare sinhix, si ottiene
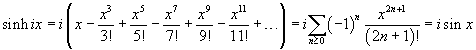
![]()
Dalle (7.21) e (3.9) si ottiene
![]()
Dalle (7.22) e (3.9) si ottiene
![]()
Riunendo il tutto
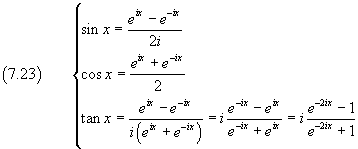
Le (7.23) sono dette formule di Eulero.
Dalle (7.23) si ottiene inoltre
![]()
La (7.24) permette di esprimere il numero complesso z, di modulo ρ e argomento θ, nei seguenti modi:
![]()
Sviluppi in serie del seno e coseno circolari con WolframAlpha.
Data la funzione
![]()
reale per x<1, le sue derivate successive sono
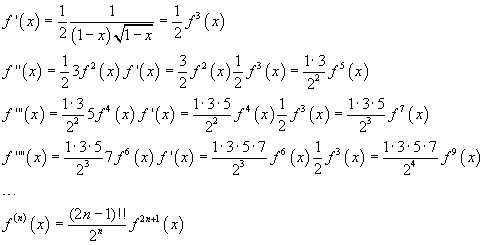
dove il doppio punto esclamativo a fianco del numero naturale positivo n ne rappresenta il doppio fattoriale, cioè
Inoltre, se n=0 o n=-1, n!! = 1.
Dato che f(0)=1, lo sviluppo in serie di MacLaurin di f(x) risulta
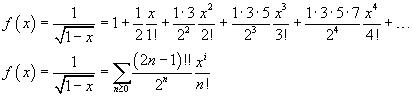
Inoltre, per -1<x<1, si ha
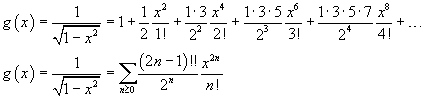
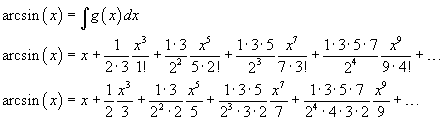
e, infine
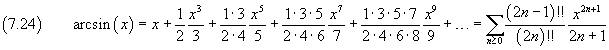
Il coseno di un angolo è uguale al seno del suo complementare, dunque
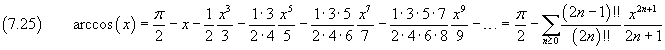
Si può ottenere lo sviluppo (7.24) in un modo più diretto se si sviluppa la funzione (7.23) usando i coefficienti binomiali generalizzati. Infatti da
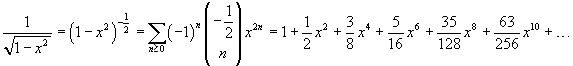
si ha
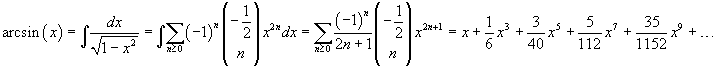
In modo analogo si può ottenere
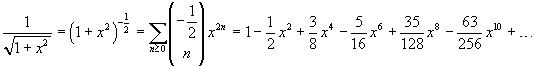
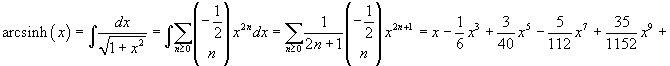
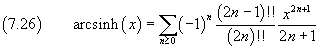
L'arcocoseno iperbolico è reale solo per x≥1. Volendo comunque un suo sviluppo in serie di MacLaurin, si può procedere nel seguente modo
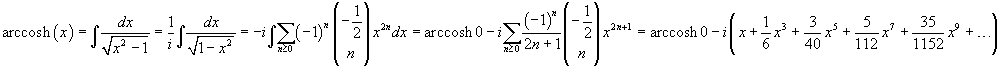
Si ha inoltre
![]()
quindi
![]()
e, in definitiva
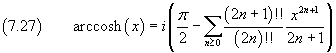
Sviluppi in serie dell'arcoseno e arcocoseno circolari con WolframAlpha.
Altri utili sviluppi in serie si trovano in Sviluppi in serie di Fourier.