L'espressione della forza nella (2.6) rende conto solo dell'effetto di un campo elettrico stazionario E su una particella di carica q ferma rispetto al sistema di riferimento in cui E è stazionario.
![]()
Ma sperimentalmente si osserva che, se q ha velocità diversa da 0 rispetto a questo sistema di riferimento, sulla carica q agisce anche la forza di Lorentz FB
![]()
dove v rappresenta la velocità della particella e quindi la forza totale agente sulla particella risulta
![]()
Come si attribuisce la forza FE alla presenza di un potenziale elettrico scalare φ(x,y,z), è possibile attribuire la forza FB alla presenza di un potenziale magnetico detto potenziale vettore, in quanto, a differenza del potenziale elettrico φ, tale potenziale magnetico ha natura vettoriale.
L'equazione di Maxwell (4.8.2) impone che la divergenza di B sia nulla
![]()
Per l'identità (5.5) la divergenza di un rotore è identicamente nulla, quindi nella (7.4) B può essere interpretato come il rotore di un qualunque campo vettoriale αA(x,y,z,t), definito a meno di un fattore reale di scala α.
Se si sostituisce questa espressione di B nell'equazione di Maxwell (4.8.3) si ottiene
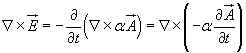
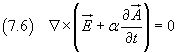
Per l'identità (5.4) il rotore
di un gradiente è identicamente nullo. Quindi, se nella (7.6) al campo
![]() si aggiunge il gradiente
di un qualunque campo scalare ψ(x,y,z,t), il rotore della somma rimane nullo:
si aggiunge il gradiente
di un qualunque campo scalare ψ(x,y,z,t), il rotore della somma rimane nullo:
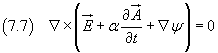
Va osservato che, come nei diversi esempi di elettrostatica proposti nella sezione 3, anche ψ risulta definito a meno di una costante additiva.
Questa proprietà dei campi elettromagnetici è detta invarianza di gauge.
Il termine inglese gauge, che esprime i concetti di misura, strumento di misura, misurare, in questo contesto assume più precisamente il significato di adeguamento di misura e viene tradotto talvolta in italiano con calibrazione. In generale, dato il suo specifico significato nelle teorie fisiche, si preferisce l'uso del vocabolo inglese.
L'invarianza di gauge consiste nel fatto che la scelta della determinazione specifica dei campi A e ψ è priva di effetti fisici osservabili e può essere intuitivamente concepita come una generalizzazione del principio per cui proprietà e leggi fisiche sono indipendenti dal particolare sistema di riferimento adottato nella descrizione dei fenomeni. Questa è una proprietà comune a molte teorie fisiche. Ad esempio nella relatività galileiana la lunghezza di una sbarra è la stessa in due sistemi di riferimento inerziali in moto l'uno rispetto all'altro con velocità relativa v (quindi in due diversi sistemi di misura): questa invarianza esprime l'assunto fisico che non esistono velocità assolute. Nella relatività einsteiniana invece le due lunghezze non coincidono in quanto si assume che la velocità della luce è assoluta e quindi invariante rispetto al sistema di riferimento.
La (7.7) implica
![]()
da cui
![]()
Quindi, in presenza di un potenziale vettore A variabile nel tempo, la forza agente su una carica q risulta
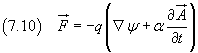
Se si vuole che l'espressione della forza nella (7.10) coincida con l'espressione della forza nella (7.3) si deve assumere
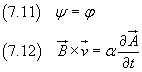
La (7.12) può aiutare a comprendere il senso fisico del potenziale A. Infatti nel caso di un campo di induzione magnetica B0 uniforme e costante
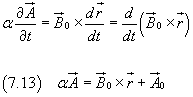
dove A0 rappresenta il valore di A in un punto qualunque dello spazio. La (7.13) esplicita il fatto che il potenziale A, come lo scalare φ, è definito a meno di una costante additiva.
Se si assume come origine O di un sistema di riferimento cartesiano un punto qualunque dello spazio e come asse z la retta per O parallela al vettore B0 orientata come B0, come A0 il valore di A in un punto di tale asse e A0=0, la (7.13) si riduce a
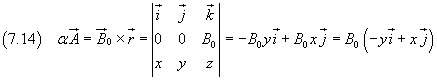
L'intensità di A in un punto P(x,y,z) risulta
![]()
A è nullo sull'asse z e la sua intensità è proporzionale alla distanza da tale asse.
Ovviamente il rotore di A deve risultare uguale a B0k:
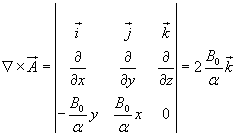
![]()
In definitiva, per produrre i risultati fisici osservabili nell'esempio proposto deve essere
![]()
Nell'esempio si è dedotta una espressione del potenziale A noto B, ma l'utilità dell'introduzione di A consiste nel processo inverso, cioè calcolare A per poi ricavare B.
Come esempio si considera il calcolo del campo di induzione B generato nel vuoto da una corrente costante I all'interno di un filo conduttore rettilineo ideale di lunghezza infinita e sezione circolare costante di raggio R. Si suppone che la densità di corrente sia costante in tutta la sezione.
Poiché I è costante, il campo elettrico E è stazionario, per cui l'equazione di Maxwell (4.8.4) nel vuoto si riduce a
![]()
Per la (7.5) si ha quindi
![]()
e per l'identità (5.11) sul rotore di rotore
![]()
Senza perdita di generalità si può assumere che la divergenza di A sia nulla (B è proporzionale al rotore di A qualunque sia la divergenza di A), quindi
Se si assume come asse z l'asse geometrico del filo orientato come la corrente I, la densità di corrente J in un punto all'interno del filo risulta
![]()
Per la (7.20)
![]()
Per la (5.10) si ha
![]()
Dato che la scelta dell'origine O del sistema di riferimento sull'asse z è arbitraria e che il sistema ha una simmetria assiale, Az dipende solo dalla distanza d del punto dall'asse del filo, quindi la (7.23) equivale a
![]()
La (7.24), analogamente all'equazione (3.26), ammette soluzione
![]()
dove Az,0 rappresenta il valore di Az sull'asse del filo. All'esterno del filo la densità di corrente è nulla, quindi
![]()
La (7.26), analogamente all'equazione (3.29), ammette soluzione
![]()
dove si assume Az nullo nei punti sulla superficie del filo. Per la continuità di Az negli stessi punti si ha
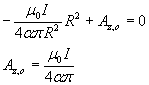
Applicando la (7.5), per i punti interni al filo si ha
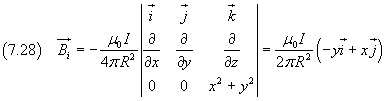
e per i punti esterni
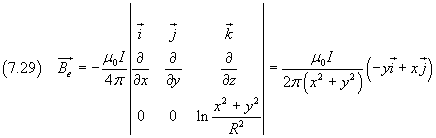
La (7.29) è nota come legge di Biot-Savart.