Ministero dell'Istruzione, dell'Università e della Ricerca
M557 - ESAME DI STATO DI ISTRUZIONE SECONDARIA SUPERIORE
Indirizzi: LI02, EA02 - SCIENTIFICO
LI03, EA09 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE

L'amministratore di un piccolo condominio deve installare un nuovo serbatoio per il gasolio da riscaldamento. Non essendo soddisfatto dei modelli esistenti in commercio, ti incarica di progettarne uno che risponda alle esigenze del condominio.

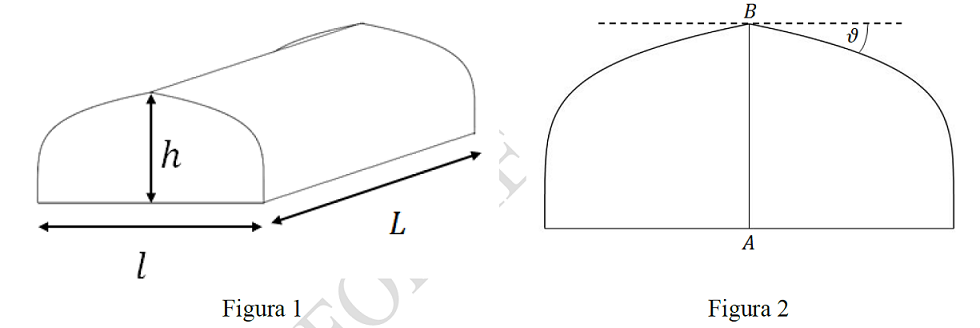
Allo scopo di darti le necessarie informazioni, l'amministratore ti fornisce il disegno in figura 1, aggiungendo le seguenti indicazioni:

• la lunghezza L del serbatoio deve essere pari a otto metri;
• la larghezza l del serbatoio deve essere pari a due metri;
• l'altezza h del serbatoio deve essere pari a un metro;
• il profilo laterale (figura 2) deve avere un punto angoloso alla sommità, per evitare l'accumulo di ghiaccio durante i mesi invernali, con un angolo θ ≥ 10°
• la capacità del serbatoio deve essere pari ad almeno 13 m³, in modo da garantire al condominio il riscaldamento per tutto l'inverno effettuando solo due rifornimenti di gasolio;
• al centro della parete laterale del serbatoio, lungo l'asse di simmetria (segmento AB in figura 2) deve essere installato un indicatore graduato che riporti la percentuale di riempimento V del volume del serbatoio in corrispondenza del livello z raggiunto in altezza dal gasolio.

1. Considerando come origine degli assi cartesiani il punto A in figura 2, individua tra le seguenti famiglie di funzioni quella che meglio può descrivere il profilo laterale del serbatoio per x ∈ [-1, 1], k intero positivo, motivando opportunamente la tua scelta:

   

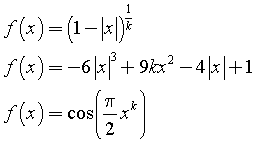
2. Determina il valore di k che consente di soddisfare i requisiti richiesti relativamente all'angolo θ e al volume del serbatoio.
3. Al fine di realizzare l'indicatore graduato, determina l'espressione della funzione V(z) che associa al livello z del gasolio (in metri) la percentuale di riempimento V del volume da riportare sull'indicatore stesso.

Quando consegni il tuo progetto, l'amministratore obietta che essendo il serbatoio alto un metro, il valore z del livello di gasolio, espresso in centimetri, deve corrispondere alla percentuale di riempimento: cioè, ad esempio, se il gasolio raggiunge un livello z pari a 50 cm vuol dire che il serbatoio è pieno al 50%; invece il tuo indicatore riporta, in corrispondenza del livello 50 cm, una percentuale di riempimento 59,7%.

4. Illustra gli argomenti che puoi usare per spiegare all'amministratore che il suo ragionamento è sbagliato; mostra anche qual è, in termini assoluti, il massimo errore che si commette usando il livello z come indicatore della percentuale di riempimento, come da lui suggerito, e qual è il valore di z in corrispondenza del quale esso si verifica.

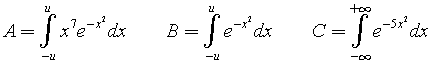
Nella figura 1 è rappresentato il grafico Γ della funzione continua , derivabile in ]0, +∞), e sono indicate le coordinate di alcuni suoi punti.

È noto che Γ è tangente all'asse y in A, che B ed E sono un punto di massimo e uno di minimo, che C è un punto di flesso con tangente di equazione .

Nel punto D la retta tangente ha equazione e per il grafico consiste in una semiretta passante per il punto G. Si sa inoltre che l'area della regione delimitata dall'arco ABCD, dall'asse x e dall'asse y vale 11, mentre l'area della regione delimitata dall'arco DEF e dall'asse x vale 1.

1. In base alle informazioni disponibili, rappresenta indicativamente i grafici delle funzioni

   

   Quali sono i valori di e ? Motiva la tua risposta.

2. Rappresenta, indicativamente, i grafici delle seguenti funzioni:

   

   specificando l'insieme di definizione di ciascuna di esse.

3. Determina i valori medi di y=f(x) e di nell'intervallo [0,8], il valore medio di nell'intervallo [1,7] e il valore medio di nell'intervallo [9,10].
4. Scrivi le equazioni delle rette tangenti al grafico della funzione F(x) nei suoi punti di ascisse 0 e 8, motivando le risposte.