Preparazione all'esame scritto di Matematica

Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario.

PROBLEMA 1

Data la funzione di equazione

1. se ne analizzino le proprietà e se ne disegni il grafico.

Sia l'equazione oraria di un punto che si muove di moto rettilineo, dove x(t) rappresenta l'ascissa, misurata in metri, del punto nell'istante generico t, misurato in secondi, rispetto all'origine data dalla sua posizione nell'istante t₀=0 secondi.

Utilizzando anche i risultati dell'analisi precedente:

2. calcolare la velocità media del punto nell'intervallo di tempo tra gli istanti t₁ =-1 sec e t₂ =1 sec.;
3. individuare il massimo valore dell'accelerazione del punto;
4. stabilire con l'approssimazione almeno del decimo di secondo l'altro istante t₃, oltre a quello iniziale t₀, in cui il punto si trova nell'origine;
5. utilizzando un linguaggio di programmazione, si scriva una procedura che permetta di approssimare t₃ a piacere.

PROBLEMA 2

Data la funzione reale di variabile reale

1. stabilire il valore da assegnare alla costante reale a perché la f(x) rappresenti la densità di distribuzione di probabilità di una variabile aleatoria continua x;
2. si rappresenti graficamente la funzione così ottenuta;
3. calcolare la deviazione standard σ della distribuzione ottenuta;
4. calcolare la probabilità che la variabile x assuma valori nell'intervallo [-σ ; σ ];
5. calcolare la probabilità che in cinque eventi la variabile aleatoria x assuma almeno una volta un valore compreso nell'intervallo [-σ ; σ ].

QUESITI

1. Data la funzione dimostrare che è invertibile su tutto R e dimostrare che la sua inversa, usualmente indicata con arcsenh x, può essere espressa come .

2. Dato un tetraedro regolare ABCD di spigolo λ=9cm, sia O il centro della base ABC e sia Σ una sezione del tetraedro parallela a tale base. Calcolare il volume massimo del tetraedro di base Σ e vertice O.

3. Calcolare le radici cubiche dell'unità immaginaria e rappresentarle nel piano di Gauss.

4. Codificare in un linguaggio di programmazione noto una funzione che calcoli la somma dei reciproci dei fattoriali dei primi n numeri naturali. A quale valore reale converge questa somma?

5. Verificare graficamente che l'equazione 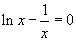ammette un'unica soluzione reale e approssimare la soluzione a meno di un centesimo.

6. In un liceo scientifico il 60% dei partecipanti all'esame di stato sono maschi e il 40% femmine. Detto v il voto di diploma, si dicono di fascia A gli studenti con v≥90, di fascia B quelli con 70≤v<90, di fascia C quelli con v<70.
Tra i maschi il 10% è di tipo A, il 70% di tipo B e il 20% di tipo C. Tra le femmine il 12% è di tipo A, il 70% di tipo B e il 18% di tipo C.
Per un'indagine campionaria sono scelti a caso cinque diplomati, 1 di fascia A, 3 di fascia B e 1 di fascia C. Qual è la probabilità che siano tutti maschi e qual è la probabilità che siano tutte femmine?

7. Dopo aver disegnato nello stesso piano cartesiano il grafico della funzione e la retta di equazione y = 1, calcolare il lato del quadrato equivalente alla figura delimita dalle due curve.

8. Stabilire per quali valori di a e b la funzione è derivabile in tutto il suo dominio.
Dimostrare che perché una funzione sia derivabile in un punto è necessario che sia continua in tale punto.

9. Valutare con un metodo di integrazione numerica la lunghezza dell'arco di cosinusoide delimitato dai suoi punti di ascissa 0 e π.

10. Due circonferenze γ₁ e γ₂ hanno ugual raggio e sono tangenti nel punto T.
Tracciati il diametro AT di γ₁ e il diametro BT di γ₂, da A si tracci una semiretta tangente a γ₂ e da B la semiretta tangente a γ₁ che intersechi la precedente semiretta nel punto C.
Calcolare il seno dell'angolo ACB.

• Problemi 1 2

• Quesiti 1 2 3 4 5 6 7 8 9 10