Y557 - ESAME DI STATO DI LICEO SCIENTIFICO
CORSO SPERIMENTALE-P.N.I.

Tema di MATEMATICA

Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario.

PROBLEMA 1

Nel piano Oxy sono date le curve λ e r di equazioni:

1. Si provi che λ e r non hanno punti comuni.
2. Si trovi il punto P∈λ che ha distanza minima da r.
3. Si determini l'area della regione finita di piano racchiusa da λ e dalla retta s, simmetrica di r rispetto all'asse x.
4. Si determini il valore di c per il quale la retta y = c divide a metà l'area della regione S del I quadrante compresa tra λ e l'asse x.
5. Si determini il volume del solido di base S le cui sezioni ottenute con piani ortogonali all'asse x sono quadrati.

svolgimento

PROBLEMA 2

Si consideri la funzione f definita sull'intervallo [0 ;+∞ [ da:

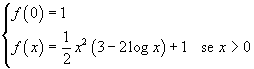
e sia C la sua curva rappresentativa nel riferimento Oxy, ortogonale e monometrico.

1. Si stabilisca se f è continua e derivabile in 0.
2. Si dimostri che l'equazione f(x) = 0 ha, sull'intervallo [0 ;+∞ [, un'unica radice reale e se ne calcoli un valore approssimato con due cifre decimali esatte.
3. Si disegni C e si determini l'equazione della retta r tangente a C nel punto di ascissa x = 1.
4. Sia n un intero naturale non nullo. Si esprima, in funzione di n, l'area A_n del dominio piano delimitato dalla curva C, dalla retta tangente r e dalle due rette: .
5. Si calcoli il limite per n → +∞ di A_n e si interpreti il risultato ottenuto.

svolgimento

QUESTIONARIO

1. Si dimostri che il lato del decagono regolare inscritto in un cerchio è sezione aurea del raggio e si utilizzi il risultato per calcolare sen18°, sen36°.

   svolgimento

2. Si dia una definizione di retta tangente ad una curva. Successivamente, si dimostri che la curva y = x sen x è tangente alla retta y = -x quando sen x =-1 ed è tangente alla retta y = -x quando sen x = -1.

   svolgimento

3. Si determinino le equazioni di due simmetrie assiali σ e φ la cui composizione σ º φ dia luogo alla traslazione di equazione:

   

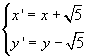
   Si determinino poi le equazioni della trasformazione che si ottiene componendo le due simmetrie in ordine inverso φ º σ.

   svolgimento

4. Una bevanda viene venduta in lattine, ovvero contenitori a forma di cilindro circolare retto, realizzati con fogli di latta. Se una lattina ha la capacità di 0,4 litri, quali devono essere le sue dimensioni in centimetri, affinché sia minima la quantità di latta necessaria per realizzarla? (Si trascuri lo spessore della latta).

   svolgimento

5. Come si definisce e quale è l'importanza del numero e di Nepero [nome latinizzato dello scozzese John Napier (1550-1617)]? Si illustri una procedura che consenta di calcolarlo con la precisione voluta.

   svolgimento

6. Le rette r e s di equazioni rispettive y = 1 + 2x e y = 2x - 4 si corrispondono in una omotetia σ di centro l'origine O. Si determini σ.

   svolgimento

7. Come si definisce n! (n fattoriale) e quale ne è il significato nel calcolo combinatorio? Quale è il suo legame con i coefficienti binomiali? Perché?

   svolgimento

8. Si trovi l'equazione della retta tangente alla curva di equazioni parametriche x = e^t + 2 e y = e^-t + 3 nel suo punto di coordinate (3, 4).

   svolgimento

9. Quale è la probabilità di ottenere 10 lanciando due dadi? Se i lanci vengono ripetuti quale è la probabilità di avere due 10 in sei lanci? E quale è la probabilità di avere almeno due 10 in sei lanci?

   svolgimento

10. Il 40% della popolazione di un Paese ha 60 anni o più. Può l'età media della popolazione di quel Paese essere uguale a 30 anni? Si illustri il ragionamento seguito per dare la risposta.

    svolgimento

_______________________________________________________________

Durata massima della prova: 6 ore.
È consentito l’uso della calcolatrice tascabile non programmabile e la consultazione del vocabolario di italiano.
Non è consentito lasciare l’Istituto prima che siano trascorse 3 ore dalla dettatura del tema.