Questionario - 2008

Quesito 1

La risposta al quesito consiste essenzialmente nel calcolo del rapporto tra il volume interno al cono ma esterno alla sfera e il volume del cono. Detto r la misura del raggio della sfera, si ha:

• volume della sfera:
• altezza del cono:
• raggio di base del cono:
• volume del cono:
• differenza tra i volumi:
• probabilità chiesta:

Quesito 2

(Questo quesito ripropone sostanzialmente il quesito 1 dell'Esame 2005)

Considerando un decagono di lato l inscritto in una circonferenza di raggio r e centro O, ognuno dei triangoli isosceli con base su un lato e vertice opposto in O è un triangolo aureo di prima specie in cui l'angolo in O misura π/5. Un qualunque angolo alla circonferenza che insista su un lato misura π/10. Per il teorema della corda si ha

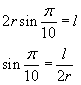
l è la sezione aurea di r: il loro rapporto è il numero aureo φ

In definitiva si ottiene

Quesito 3

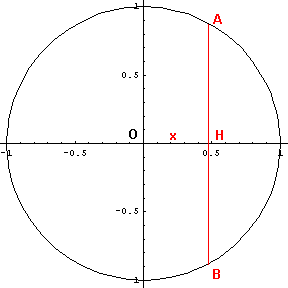
Con riferimento alla figura, sia AB una corda parallela a un diametro assunto come asse delle ordinate di un sistema cartesiano ortogonale con origine nel centro O della circonferenza. Detta x la distanza OH, il segmento AH ha misura

Il triangolo equilatero con base AB ha altezza

L'area del triangolo risulta quindi

Il volume chiesto è dato da

Quesito 4

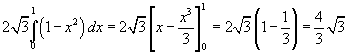
Se due funzioni f(x) e g(x) per x che tende ad un punto di accumulazione x₀ comune ai loro domini tendono a 0 e in x₀ la g'(x) non si annulla, allora .

Le condizioni sono soddisfatte dal numeratore e dal denominatore e da tutte le loro derivate. La derivata di ordine 2008 del numeratore è nulla, mentre quella del denominatore non si annulla. Dunque il limite è 0.

Quesito 5

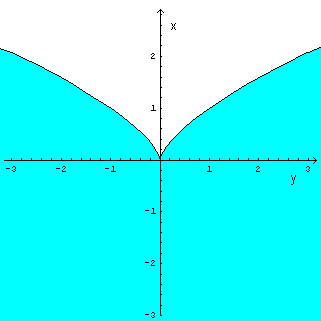
La curva di equazione divide il piano in due regioni, di cui una soddisfa al vincolo imposto.

Grafico della curva

• La funzione è reale per ogni valore reale di y; è pari, quindi il suo diagramma è simmetrico rispetto all'asse delle x e ha un minimo relativo per y=0, cioè nell'origine; diverge positivamente per y→±∞.

• La derivata prima di x rispetto a y è , dunque la x non è derivabile per y=0.

  Poiché , nell'origine c'e una cuspide.

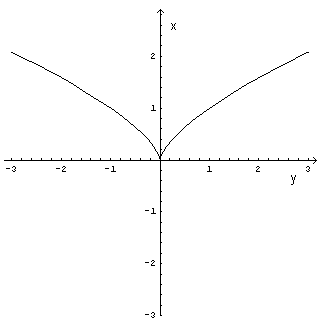
Il punto (1;0) verifica la disequazione, quindi la verificano tutti i punti della stessa regione.

Quesito 6

Si possono rappresentare i tre spigoli del parallelepipedo con tre vettori tridimensionali applicati all'origine . La diagonale è rappresentata dalla loro somma: . Il modulo della diagonale è .

I coseni dei tre angoli chiesti si ottengono dividendo i prodotti scalari tra diagonale e lato per i prodotti dei moduli degli stessi vettori.

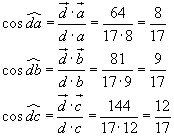
Si ha quindi

Quesito 7

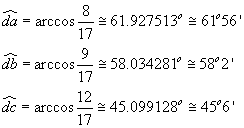
(Questo quesito ripropone sostanzialmente il quesito 5 dell'Esame 2007)

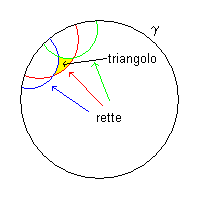
Si dicono 'non euclidee' le geometrie nelle quali non vale il cosiddetto quinto postulato di Euclide: dati nel piano una retta e un punto esterno ad essa, per il punto passa una e una sola parallela alla retta data. Sostituendo a questo postulato affermazioni alternative, si possono costruire sistemi coerenti di proposizioni geometriche, detti appunto geometrie non euclidee, come quelle proposti da Gauss, Lobachevsky e Riemann.

Queste geometrie sono dette iperboliche se ammettono l'esistenza di infinite parallele, ellittiche se non ammettono parallele.

Ad esempio, un modello intuitivo della geometria ellittica di Riemann può essere rappresentato considerando come 'piano' una superficie sferica e come 'rette' le circonferenze di diametro uguale a quello della sfera. Ipotizzando un globo terrestre perfettamente sferico, tutti i meridiani e l'equatore sarebbero 'rette'. Si comprende facilmente che il 'triangolo' formato da due meridiani e l'equatore è tale da avere la somma degli angoli interni maggiore di un angolo piatto, in quanto gli angoli che i meridiani formano con l'equatore sono entrambi retti e alla loro somma va aggiunto l'angolo formato dai meridiani nel polo in cui si incontrano.

Come modello intuitivo di geometria iperbolica si può citare il modello di Poincaré, in cui si considera come 'piano' la superficie di un cerchio Γ delimitato dalla circonferenza γ e 'rette' gli archi di circonferenza interni a Γ, con estremi su γ con tangenti negli estremi coincidenti con raggi di γ. In questo modello si vede che nei 'triangoli' la somma degli angoli interni è minore di un angolo piatto.

Quesito 8

Le funzioni esponenziali con base x diversa dalla base naturale e sono tali che , dunque , quindi x^π, come il logaritmo naturale, è reale solo se x è positivo. Di conseguenza anche la f, in cui il minuendo è reale per ogni argomento reale, è reale solo per per argomenti positivi.

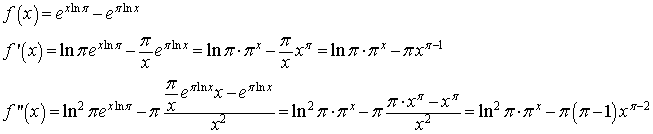
I valori delle derivate per x=π sono

Quesito 9

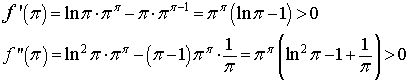
I gruppi di 8 studenti, distinti solo dalla composizione, che possono essere formati con 20 studenti sono . I gruppi formati da quattro femmine e quattro maschi sono . La probabilità chiesta è data dal rapporto tra casi favorevoli e casi possibili.

Quesito 10

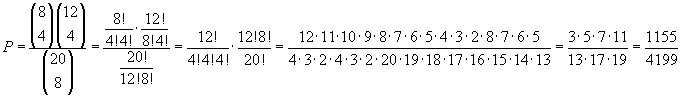
Dato il punto P(x,y), il suo simmetrico rispetto all'origine è P'(-x,-y). La curva simmetrica rispetto all'origine ha quindi equazione .

Il simmetrico di P(x,y) rispetto alla bisettrice dei quadranti dispari è P'(y,x). La curva simmetrica rispetto alla bisettrice dei quadranti dispari della curva assegnata ha quindi equazione