Y557 - ESAME DI STATO DI LICEO SCIENTIFICO
CORSO SPERIMENTALE
Indirizzo: PIANO NAZIONALE INFORMATICA

Tema di MATEMATICA

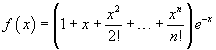
Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario.

PROBLEMA 1

Sia f la funzione definita da

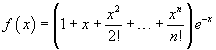
dove n è un intero positivo e x ∈ R.

1. Si verifiche che la derivata di f(x) è:
2. Si dica se la funzione f ammette massimi e minimi (assoluti e relativi) e si provi che, quando n è dispari, per ogni x reale.
3. Si studi la funzione g ottenuta da f quando n = 2 e se ne disegni il grafico.
4. Si calcoli e se ne dia l'interpretazione geometrica.

svolgimento

PROBLEMA 2

In un sistema di riferimento cartesiano ortogonale Oxy, si consideri la funzione definita da , con k parametro reale.

1. Si dica come varia il grafico di f al variare di k (k positivo, negativo o nullo).
2. Sia e γ il suo grafico. Si dimostri che γ e la retta di equazione hanno un solo punto P in comune. Si determini l'ascissa di P approssimandola a meno di 0,1 con un metodo iterativo di calcolo.
3. Sia D la regione finita del primo quadrante delimitata da γ e dal grafico della funzione inversa di g. Si calcoli l'area di D.
4. La regione D è la base di un solido W le cui sezioni con i piani perpendicolari alla bisettrice del primo quadrante sono tutte rettangoli di altezza 12. Si determini la sezione di area massima. Si calcoli il volume di W.

svolgimento

QUESTIONARIO

1. Siano e . Si provi che

   svolgimento

2. Sono dati gli insiemi e . Tra le possibili funzioni (o applicazioni) di A in B, ce ne sono di suriettive? Di iniettive?. Di biiettive?

   svolgimento

3. Una moneta da 2 euro (il suo diametro è 25,75 mm) viene lanciata su un pavimento ricoperto con mattonelle quadrate di lato 10 cm. Quale è la probabilità che la moneta vada a finire internamente ad una mattonella? (cioè non tagli i lati dei quadrati)

   svolgimento

4. "Esiste solo un poliedro regolare la cui facce sono esagoni". Si dica se questa affermazione è vera o falsa e si fornisca una esauriente spiegazione della risposta.

   svolgimento

5. Si considerino le seguenti espressioni:

   

   A quali di esse è possibile attribuire un valore numerico? Si motivi la risposta.

   svolgimento

6. Con l'aiuto di una calcolatrice, si applichi il procedimento iterativo di Newton all'equazione , con punto iniziale . Cosa si ottiene dopo due iterazioni?

   svolgimento

7. Si dimostri l'identità con n e k naturali e n > k.

   svolgimento

8. Alla festa di compleanno di Anna l'età media dei partecipanti è di 22 anni. Se l'età media degli uomini è 26 anni e quella delle donne è 19, qual è il rapporto tra il numero degli uomini e quello delle donne?

   svolgimento

9.  

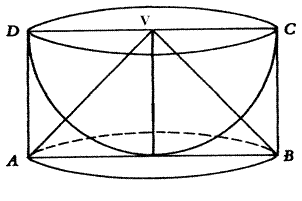   Nei "Discorsi e dimostrazioni matematiche intorno a due nuove scienze", Galileo Galilei descrive la costruzione di un solido che chiama scodella considerando una semisfera di raggio r e il cilindro ad essa circoscritto. La scodella si ottiene togliendo la semisfera dal cilindro. Si dimostri, utilizzando il principio di Cavalieri, che la scodella ha volume pari al cono di vertice V in figura.

   svolgimento

10.  

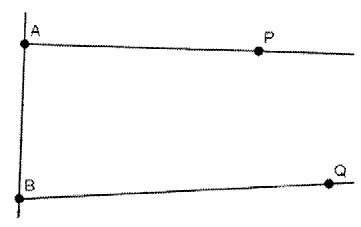
    "Se due punti P e Q del piano giacciono dalla stessa parte rispetto ad una retta AB e gli angoli hanno somma minore di 180°, allora le semirette AP e BQ, prolungate adeguatamente al di là dei punti P e Q, si devono intersecare.". Questa proposizione è stata per secoli oggetto di studio da parte di schiere di matematici. Si dica perché e con quali risultati.

    svolgimento

_______________________________________________________________

Durata massima della prova: 6 ore.
È consentito soltanto l’uso della calcolatrice non programmabile.
Non è consentito lasciare l’Istituto prima che siano trascorse 3 ore dalla dettatura del tema.