Y557 - ESAME DI STATO DI LICEO SCIENTIFICO
CORSO SPERIMENTALE
Indirizzo: PIANO NAZIONALE INFORMATICA

Tema di MATEMATICA

Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario.

PROBLEMA 1

Nella figura che segue è riportato il grafico di per essendo g la derivata di una funzione f. Il grafico consiste di tre semicirconferenze con centri in e raggi rispettivi .

1. Si scriva un'espressione analitica di . Vi sono punti un cui non è derivabile? Se si, quali sono? E perché?
2. Per quali valori di x, , la funzione f presenta un massimo o un minimo relativo? Si illustri il ragionamento seguito.
3. Se , si determini f(4) e f(1).
4. Si determinino i punti in cui la funzione f ha derivata seconda nulla. Cosa si può dire sul segno di f? Qual è l'andamento qualitativo di f(x)?

svolgimento

PROBLEMA 2

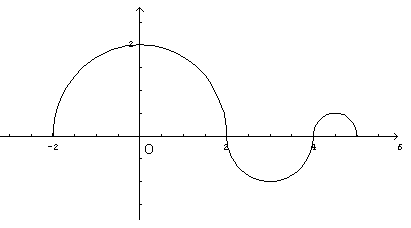
Nel piano riferito ad un sistema Oxy di coordinate cartesiane siano assegnate le parabole di equazioni e .

1. Si disegninino le due parabole e se ne determinino le coordinate dei fuochi e le equazioni delle rispettive rette direttrici. Si denoti conA il puntod'intersezione delle due parabole diverso dall'origine O.
2. L'ascissa di A è ; si dica a quale problema classico dell'antichità è legato tale numero e, mediante l'applicazione di un metodo iterativo di calcolo, se ne trovi il valore approssimato a meno di 10^-2.
3. Sia D la parte di piano delimitata dagli archi delle due parabole di estremi O e A. Si determini la retta r, parallela all'asse delle x, che stacca su D il segmento di lunghezza massima.
4. Si consideri il solido W ottenuto dalla rotazione di D intorno all'asse x. Se si taglia W con piani ortogonali all'asse x, quale forma hanno le sezioni ottenute? Si calcoli il volume di W.

svolgimento

QUESTIONARIO

1. Sia p(x) un polinomio di grado n. Si dimostri che la sua derivata n-esima è dove a_n è il coefficiente di xⁿ.

   svolgimento

2. Siano ABC un triangolo rettangolo in A, r la retta perpendicolare in B al piano del triangolo e P un punto di r distinto da B. Si dimostri che i tre triangoli PAB, PBC, PCA sono triangoli rettangoli.

   svolgimento

3. Sia r la retta di equazione tangente al grafico di . Qual è la misura in gradi e primi sessagesimali dell'angolo che la retta r forma con il semiasse positivo delle ascisse?.

   svolgimento

4. Si calcoli con la precisione di due cifre decimali lo zero della funzione . Come si può essere certi che esiste un unico zero?

   svolgimento

5. Sia g il grafico di una funzione . Si illustri in che modo è possibile stabilire se G è simmetrico rispetto alla retta .

   svolgimento

6. Si trovi l'equazione cartesiana del luogo geometrico descritto dal punto P di coordinate al variare di t, .

   svolgimento

7. Per la ricorrenza della festa della mamma, la sig.ra Luisa organizza una cena a casa sua, con le sue amiche che hanno almeno una figlia femmina. La sig.ra Anna è una delle invitate e perciò ha almeno una figlia femmina. Durante la cena, la sig.ra Anna dichiara di avere esattamente due figli. Si chiede: qual è la probabilità che anche l'altro figlio della sig.ra Anna sia femmina? Si argomenti la risposta.

   svolgimento

8. Se n>3 e sono in progressione aritmetica, qual è il valore di n?.

   svolgimento

9. Si provi che non esiste un triangolo ABC con . Si provi altresì che se , allora esistono due triangoli che soddisfano queste condizioni.

   svolgimento

10. Si consideri la regione finita di piano delimitata da , dall'asse x e dalla retta .

    L'integrale fornisce il volume del solido:

    1. generato da r nella rotazione intorno all'asse delle x;
    2. generato da r nella rotazione intorno all'asse delle y;
    3. di base R le cui sezioni con i piani perpendicolari all'asse x sono semicerchi di raggio ;
    4. nessuno di questi;

    Si motivi esaurientemente la risposta.

    svolgimento

_______________________________________________________________

Durata massima della prova: 6 ore.
È consentito soltanto l’uso della calcolatrice non programmabile.
Non è consentito lasciare l’Istituto prima che siano trascorse 3 ore dalla dettatura del tema.