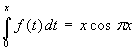Y557 - ESAME DI STATO DI LICEO SCIENTIFICO
PIANO NAZIONALE DI INFORMATICA
CORSO SPERIMENTALE

Tema di MATEMATICA

Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario.

PROBLEMA 1

Due numeri x e y hanno somma e quoziente uguali ad un numero reale a non nullo.
Riferito il piano ad un sistema S di coordinate cartesiane ortogonali e monometriche (x,y):

1. si interpreti e discuta il problema graficamente al variare di a;
2. si trovi l'equazione cartesiana del luogo γ dei punti P(x,y) che soddisfano al problema;
3. si rappresentino in S sia la curva γ che la curva γ' simmetrica di γ rispetto alla bisettrice del I e del III quadrante;
4. si determini l'area della regione finita di piano del primo quadrante delimitata da γ e γ' e se ne dia un'approssimazione applicando uno dei metodi numerici studiati;
5. si calcoli y nel caso che x sia uguale a 1 e si colga la particolarità del risultato.

 Svolgimento

PROBLEMA 2

I raggi OA = OB = 1 metro tagliano il cerchio di centro O in due settori circolari, ciascuno dei quali costituisce lo sviluppo della superficie laterale di un cono circolare retto.
Si chiede di determinare:

1. il settore circolare (arco, ampiezza e rapporto percentuale con il cerchio) al quale corrisponde il cono C di volume massimo, il valore V di tale volume massimo e il valore V' assunto in questo caso dal volume del secondo cono C';
2. la capacità complessiva, espressa in litri, di C e di C';
3. un'approssimazione della misura, in gradi sessagesimali, dell'angolo di apertura del cono C, specificando il metodo numerico che si utilizza per ottenerla.

 Svolgimento

QUESTIONARIO

1. Se a e b sono numeri positivi assegnati quale è la loro media aritmetica? Quale la media geometrica? Quale delle due è più grande? E perché? Come si generalizzano tali medie se i numeri assegnati sono n?

   Svolgimento

2. Il seguente è uno dei celebri problemi del Cavaliere di Méré (1610 - 1685), amico di Blaise Pascal: giocando a dadi è più probabile ottenere almeno una volta 1 con 4 lanci di un solo dado, oppure almeno un doppio 1 con 24 lanci di due dadi?

   Svolgimento

3. Assumendo che i risultati - X, 1, 2 - delle 13 partite del Totocalcio siano equiprobabili, calcolare la probabilità che tutte le partite, eccetto una, terminino in parità.

   Svolgimento

4. Calcolare

   

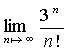
   Svolgimento

5. Cosa si intende per funzione periodica? Quale è il periodo di

   

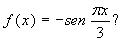
   Quale quello di sen2x?

   Svolgimento

6. Utilizzando il teorema di Rolle, si verifichi che il polinomio

   

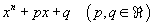
   se n è pari ha al più due radici reali, se n è dispari ha al più tre radici reali.

   Svolgimento

7. Data la funzione

   

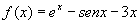
   calcolarne i limiti per x tendente a +∞ e -∞ e provare che esiste un numero reale α con 0< α < 1 in cui la funzione si annulla.

   Svolgimento

8. Verificare che la funzione

   

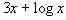
   è strettamente crescente. Detta g la funzione inversa, calcolare

   

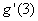
   Svolgimento

9. Trovare f(4) sapendo che

   

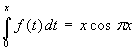
   Svolgimento

10. Spiegare, con esempi appropriati, la differenza tra omotetia e similitudine nel piano.

    Svolgimento

_______________________________________________________________

Durata massima della prova: 6 ore.

È consentito l'uso della calcolatrice tascabile non programmabile e la consultazione del vocabolario di italiano.

Non è consentito lasciare l'Istituto prima che siano trascorse 3 ore dalla dettatura del tema.
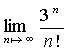