La meccanica newtoniana si fonda sui tre noti principi, il primo dei quali, noto come principio di inerzia, è comunemente enunciato nei testi scolastici nel seguente modo: un punto libero, se è fermo, continua a stare fermo, se è in movimento, continua a muoversi di moto rettilineo uniforme.
Questa proposizione può apparire banale agli studenti (e forse anche agli autori dei libri di testo) e questa sensazione può essere giustificata dal fatto che, dopo la sua rituale enunciazione, praticamente scompare dalla didattica.
Invece il senso fondamentale di questo enunciato non è per nulla banale: ne è una prova il fatto che è stato formulato solo nel XVII secolo e che c'è voluto il genio di Galileo e di Newton per arrivare a concepirlo con chiarezza, e trecento anni dopo, quello di Einstein per svilupparne tutte le implicazioni e arrivare a conclusioni assolutamente divergenti rispetto a quanto suggerito dal senso comune.
La dizione punto libero vuol denotare un corpo puntiforme, dotato di massa finita e costante m, non condizionato da nessuna presenza esterna, il cui comportamento non è diverso da quello che avrebbe se fosse solo in tutto l'universo.
Bisogna notare che questa è una grossa astrazione rispetto alla concreta esperienza delle cose.
Per esempio, in natura non esistono corpi puntiformi: ogni corpo, piccolo o grande, ha comunque un'estensione. Ma, peggio, l'idea stessa di corpo puntiforme è un assurdo teorico: un tale corpo avrebbe densità infinita.
Comunque in tutto l'Universo non esistono punti liberi, perché tutti i corpi dell'Universo sono sottoposti all'attrazione gravitazionale di altri corpi.
Ma il concetto di punto libero e il primo principio permettono di impostare lo studio del movimento, cioè della meccanica, in modo analogo a quello in cui Euclide aveva impostato lo studio delle proprietà spaziali dei corpi: punti, rette, figure piane e solide, per Euclide, non sono oggetti dell'esperienza, ma oggetti del pensiero, le cui reciproche relazioni sono deducibili dai suoi famosi cinque postulati.
Ad esempio, le seguenti proposizioni:
non ci dicono tanto cosa sono punti e rette, la cui definizione porta ai paradossi evidenziati da Zenone, ma specificano le relazioni che si assume esistano tra questi oggetti e, in modo implicito, quali sono le proprietà dell'entità che li contiene, cioè dello spazio geometrico.
In modo analogo, il concetto di punto libero e il primo principio permettono di fondare una teoria del movimento soprattutto perché definiscono implicitamente le proprietà delle entità teoriche necessarie per la sua descrizione univoca e completa: spazio, tempo, sistemi di riferimento.
Il principio di inerzia postula implicitamente le proprietà dello spazio: esso è assoluto, omogeneo e isotropo.
In effetti, dire che un punto libero (ammesso che possa esistere) se è fermo, continua a stare fermo, è lo stesso che dire: "Indipendentemente dalla posizione in cui si trova (omogeneità), un corpo libero fermo non ha una direzione preferenziale da percorrere (isotropia), per cui non può che stare fermo.
Per i filosofi aristotelici contemporanei di Galilei un corpo, ovunque lo si ponesse, si sarebbe dovuto mettere subito in movimento per raggiungere il suo "luogo naturale" (a meno di non trovarsi già in tale punto speciale).
Il principio di inerzia afferma inoltre che, sia che un punto sia fermo, sia che si muova di moto rettilineo uniforme, mantiene il suo stato di moto, cioè non c'è sostanziale differenza tra queste due situazioni, cioè il moto rettilineo uniforme è indistinguibile dalla quiete.
Per essere sicuri che un corpo è fermo, bisognerebbe controllare che la sua posizione non varia rispetto ad un altro corpo sicuramente fermo. Insomma, dovrebbe essere possibile verificare l'esistenza di un altro corpo assolutamente fermo.
Per gli aristotelici la cosa era scontata: per loro un corpo sicuramente fermo c'era: era appunto il centro dell'Universo, cioè il centro della la Terra. Ma da quando Copernico ha detronizzato la Terra dal suo ruolo privilegiato di corpo immobile al centro dell'universo, essa non è più stata sostituita da niente.
Insomma è impossibile parlare di quiete assoluta di un punto e quindi di un sistema di riferimento ancorato ad esso e quindi è impossibile stabilire la quiete assoluta (e quindi il moto assoluto) di un punto. Il massimo che si può dire è che un punto P è in quiete rispetto ad un sistema di riferimento O: lo stesso punto P, descritto rispetto ad un altro sistema di riferimento O', in moto rispetto al primo, apparirà in movimento.
Ad esempio, alberi e case sono fermi rispetto alla Terra, ma visti da un treno in movimento, appaiono in moto con velocità contraria a quella che il treno ha rispetto alla Terra.
E spesso nelle stazioni succede, guardando fuori dai finestrini del proprio treno, di non capire se è il nostro treno che si muove (rispetto alla Terra) o quello del binario accanto.
Questa confusione, che può sembrare un inganno dei sensi, è invece inevitabile e basilare nella teoria newtoniana.
In queste occasioni, riusciamo a capire che è il nostro treno che si muove accelerando, solo se osserviamo su di noi o sugli oggetti del nostro scompartimento delle forze non giustificate da interazioni con altri corpi, che, ad esempio, ci rendono difficile mantenere l'equilibrio o fan cadere le valigie.
Se non si osservano tali forze (dette "fittizie"), allora si dice che il sistema di riferimento è inerziale.
Ma queste forze si osservano solo quando il nostro treno accelera o frena.
Quando il nostro treno (supposto dotato di ottimi ammortizzatori) va a velocità costante rispetto alla Terra, se teniamo chiusi i finestrini e osserviamo solo ciò che succede all'interno del nostro scompartimento, non abbiamo nessun segnale sicuro del movimento del treno stesso rispetto alla Terra: possiamo camminare, versarci un bicchiere d'acqua o lanciare oggetti esattamente come fossimo fermi rispetto alla Terra.
Quindi il primo principio della dinamica stabilisce implicitamente l'esistenza (almeno teorica) di sistemi inerziali e l'inconsistenza teorica del concetto di moto assoluto.
Stabilisce in definitiva un principio noto come principio di relatività galileiana: se un sistema O' (nell'esempio, il treno) si muove con velocità costante rispetto ad un sistema supposto inerziale O (nell'esempio, la Terra), anche O' è un sistema inerziale e non c'é modo di capire, con osservazioni interne ad O', se tale sistema è in quiete o in movimento rispetto ad O.

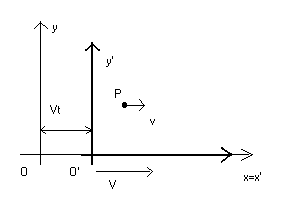
Per formalizzare questi ragionamenti, si consideri un sistema inerziale con origine O e un sistema con origine O' in moto rispetto ad O con una velocità costante V, parallela all'asse delle ascisse del sistema O (tale velocità V è detta velocità di trascinamento).
Se per semplicità si assume che, all'istante t0=0, O' coincide con O, allora, dopo un tempo t, O' si troverà ad una distanza X = Vt da O.
Dunque, al tempo t, se un punto P ha ascissa x rispetto ad O, avrà ascissa x'=x-X rispetto ad O', cioè x'=x-Vt.
Le altre coordinate y e z di P rispetto ad O rimangono invariate nel cambiamento di sistema, quindi y'=y e z'=z.
Ma bisogna osservare che nella fisica di Galileo e di Newton, come nell'intuizione ingenua, si dà per scontata un'altra cosa che si rivelerà discutibile: il tempo t è lo stesso per i due sistemi, cioè se nel sistema O è trascorso un tempo t allora nel sistema O' è trascorso un tempo t' = t.
Quindi, nei fondamenti della meccanica newtoniana è implicita quest'altra assunzione: il tempo è lo stesso per tutti gli osservatori, non dipende dal sistema di riferimento. In particolare, se due eventi sono simultanei per un osservatore, lo sono per qualunque altro osservatore.
In definitiva la meccanica newtoniana si fonda implicitamente sulle seguenti assunzioni:
Dati due sistemi inerziali O e O', con O' che si muove con velocità di trascinamento positiva V lungo l'asse delle x del sistema O, le coordinate spazio-temporali di un punto P, passando dal sistema di riferimento O al sistema di riferimento O' cambiano in questo modo:
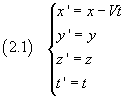
Le relazioni (2.1) sono note come trasformazioni di Galileo.
Se il punto P non è fermo rispetto ad O, ma si muove con velocità positiva costante v parallelamente all'asse x, quale sarà la velocità v' dello stesso punto vista da O' ? La risposta dovrebbe essere abbastanza immediata
![]()
La (2.2) esprime il principio di addizione delle velocità, ed è abbastanza agevole desumerlo dalle trasformazioni di Galileo:
![]()
Ovviamente si può anche dire
![]()
Ad esempio, se O' è un treno che si muove rispetto alla Terra con una velocità V = 30 m/s e P è passeggero che si muove sul treno con una velocità v' = 2 m/s rispetto al pavimento del treno, allora la velocità v del passeggero rispetto alla Terra è di 32 m/s.
Se il passeggero sul treno accelera uniformemente passando da una velocità v'1 al tempo t'1 ad una velocità v'2 al tempo t'2, la sua accelerazione a' risulta
![]()
Cioè in due sistemi di riferimento inerziali le accelerazioni risultano uguali.
Per il secondo principio della dinamica le accelerazioni sono dovute a forze ad esse direttamente proporzionali. Il coefficiente di proporzionalità è la massa inerziale del punto.
Se oltre ai tre principi di Newton si assume anche il principio di conservazione della massa, cioè che la massa è una proprietà costante specifica di un punto, indipendente dal sistema di riferimento, dalla uguaglianza delle accelerazioni e dalla costanza della massa, si desume la uguaglianza delle forze nei sistemi di riferimento inerziali.
Quindi se si sta sul treno (O') o si sta a terra (O), si vedono forze uguali produrre effetti uguali.
Questo fatto può essere espresso dicendo che le leggi della meccanica classica sono covarianti rispetto alle trasformazioni di Galileo.
Fino a che ci si limitò alla descrizione del moto di oggetti materiali come pianeti o molecole o parti di macchine come orologi o motori, la meccanica newtoniana nei suoi presupposti espliciti e impliciti funzionò più che egregiamente avvalorando quindi i principi su cui si basava fino a renderli senso comune, evidenti, indubitabili.
Fu dallo studio delle leggi dell'ottica e delle proprietà della luce nell'Ottocento, che cominciarono a sorgere i primi problemi e i primi dubbi che divennero dirompenti con lo sviluppo dello studio dell'elettromagnetismo e con la formulazione da parte di Maxwell delle equazioni fondamentali dell'elettrodinamica (seconda metà dell'800).
Per limitarsi all'ottica, il problema più dirompente risultò quello della misura della velocità della luce.
Già Galileo, in polemica con gli aristotelici (ma anche con Cassini e Descartes), sosteneva che la luce si propaga nello spazio con velocità finita e si sforzò di comprovare sperimentalmente questa sua affermazione: non ci riuscì perché i mezzi tecnici dell'epoca non permettevano la precisione necessaria per questa misura.
Dopo le prime imprecise misure astronomiche di Roemer, che portarono comunque a concludere che la velocità della luce è finita, Fizeau e Foucault, a metà dell'800, trovarono con metodi di laboratorio per la velocità della luce nel vuoto un valore molto più preciso, prossimo a 300.000 Km/s, comunemente indicato con c.
In analogia con le onde sonore, molti fisici pensavano che la luce, essendo un'onda, potesse esistere solo come oscillazione di un mezzo elastico continuo che riempie l'Universo, che chiamarono etere, e che la velocità c della luce dovesse interpretarsi definita rispetto all'etere, supposto immobile.
La congettura di un etere immobile appare subito in contraddizione con i fondamenti della meccanica: si è visto che il concetto di immobilità assoluta non è ammissibile nella fisica moderna.
Ma i principi non sono dogmi inviolabili: accettando in via provvisoria questa ipotesi bisogna però concludere che, se l'etere esiste ed è fermo, nei sistemi inerziali in moto con velocità V equiversa con la direzione di propagazione di un raggio luminoso, per la relatività galileiana (eq. 2.2) la luce dovrebbe avere velocità c'=c-V.
Il problema fu attentamente studiato con strumentazione sempre più raffinata soprattutto dai fisici statunitensi A.A. Michelson e E. W. Morley, intenzionati ad evidenziare l'esistenza dell'etere.
I risultati negativi delle loro misure indussero A. Einstein a negare definitivamente l'esistenza dell'etere ma anche a perfezionare il principio di relatività galileiana, affermando che la velocità della luce nel vuoto è la stessa in tutti i riferimenti inerziali, cioè che la velocità della luce non si compone con la velocità di trascinamento. Infatti, se in un sistema di riferimento si osservasse una velocità della luce c' diversa da c, sarebbe possibile dedurre il moto assoluto del sistema, in palese contraddizione con il Principio di Relatività.
Einstein però, per ribadire e perfezionare il Principio di Relatività, dovette negare uno degli assunti impliciti fondamentali della meccanica newtoniana, cioè l'assolutezza del tempo, sostituendolo con il principio dell'assolutezza della velocità della luce.
L'obiettivo di questi fisici era quello di verificare che la velocità della luce c si compone con la
velocità V di traslazione della Terra nel suo moto annuo attorno al Sole. A tale scopo progettarono e
usarono uno strumento, detto interferometro, basato sulla interferenza di due raggi luminosi, prodotti dallo
sdoppiamento di un unico raggio di lunghezza d'onda λ tramite uno specchio semiriflettente,
caratterizzati da cammini ottici diversi.
Dove la differenza tra i cammini ottici è un numero intero di λ, l'interferenza è costruttiva;
quando la differenza tra i cammini ottici è un numero dispari di λ/2 l'interferenza è distruttiva.
L'interferometro, solidale con la Terra, partecipa del suo moto di traslazione e si muove verso destra con velocità V.
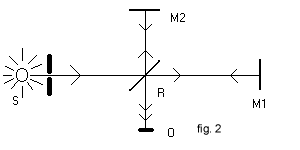
Riferendosi alla figura 2, S è la sorgente. Un raggio incide sullo specchio semiriflettente in R, che forma un angolo di 45° rispetto al raggio. Metà raggio attraversa lo specchio, incide sullo specchio riflettente M1, ritorna ad incidere in R e perviene allo schermo di osservazione O. L'altra metà del raggio è riflessa, incide sullo specchio riflettente M2 ed è riflessa, attraversa R e perviene in O interferendo con la metà precedente.
Indicando con d1 la distanza RM1 e con d2 la distanza RM2 e ammettendo la composizione galileiana delle velocità, bisogna ammettere che il raggio RM1, rispetto alla scatola, all'andata ha velocità c-V e al ritorno ha velocità c+V. Il tempo totale t1 che esso impiega a percorrere il tragitto RM1R risulta
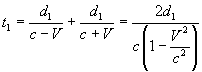
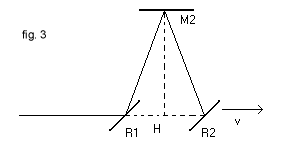
Per il calcolo delle durata t2 del tragitto RM2R dell'altro mezzo raggio bisogna osservare (fig. 3) che il percorso di andata RM2 e il percorso di ritorno ritorno M2R non si sovrappongono, perché lo specchio R è in moto: il percorso R1M2 non è perpendicolare a V, ma forma l'ipotenusa di un triangolo rettangolo di cateti M2H e R1H.
Per il teorema di Pitagora
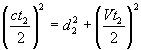
da cui si ricava
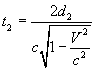
I tempi t1 e t2 risultano diversi, cioè i due raggi arrivano in O sfasati producendo una sequenza di frange di interferenza.
Se si ruota l'interferometro di un angolo retto, nei due valori di t, d1 si scambia con d2, lo sfasamento sarebbe diverso e si dovrebbe ottenere una diversa figura di interferenza.
Ma ciò non succedeva. Einstein ne dedusse che era sbagliato il presupposto, cioè la composizione di c con V dovuta all'ipotesi dell'esistenza dell'etere come sistema di riferimento assoluto, e decise di riformare le trasformazioni di Galileo in modo da rispettare il principio della assolutezza della velocità c.
(Questo paragrafo e il seguente possono essere sostituiti da una deduzione più semplice delle equazioni di Lorentz)
Nei corsi di trigonometria si introducono le funzioni circolari sinα, cosα, tanα caratterizzate dalle seguenti relazioni fondamentali:
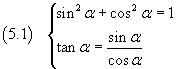
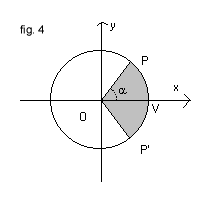
La prima di tali relazioni è state dedotta osservando (fig. 4) che ad ogni angolo antiorario α con vertice nell'origine O e primo lato coincidente con l'asse x corrisponde biunivocamente un punto P(x,y) della circonferenza trigonometrica x2+y2=1 e quindi le coordinate x e y sono funzioni parametriche di tale angolo.
Si è quindi posto
![]()
e si sono sostituite le espressioni di parametriche x e y alle variabili dell'equazione della circonferenza trigonometrica.
Va notato che il parametro α, oltre che come ampiezza dell'angolo POV, può essere geometricamente interpretato come area del settore circolare POP' dove P' è il punto simmetrico di P rispetto all'asse delle ascisse.
Una rotazione del piano cartesiano attorno all'origine è una trasformazione in cui ogni circonferenza corrisponde a se stessa.
Le equazioni di una rotazione di angolo α sono
![]()
In effetti, elevando al quadrato entrambi i membri delle equazioni (5.3) e sommando membro a membro si ottiene appunto x' 2+y' 2=x2+y2
In modo del tutto analogo si consideri (fig. 5) nel piano cartesiano l'iperbole equilatera di equazione x2-y2=1.
Questa iperbole è costituita da due rami simmetrici rispetto all'asse delle ordinate di cui quello destro interseca l'asse x nel punto V.
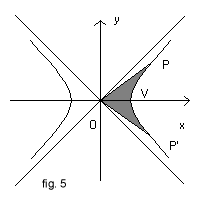
Si considerino un punto P(x,y) del ramo destro dell'iperbole e il suo simmetrico P' rispetto all'asse delle ascisse. Si traccino i segmenti PO e OP'. Si consideri la figura delimitata dai segmenti PO, OP' e dall'arco di iperbole PVP'. Interpretando come positiva l'area α di questa figura POP' quando P è nel primo quadrante e negativa la stessa area quando P è nel quarto quadrante, si possono interpretare le coordinate x e y di P come funzioni parametriche di α.
La funzione che dà l'ascissa è detta coseno iperbolico (cosh), quella che dà l'ordinata è detta seno iperbolico (sinh).
![]()
Sostituendo tali funzioni alle variabili dell'equazione dell'iperbole e denominando tangente iperbolica (tanh) il rapporto tra seno e coseno iperbolici, si ottengono le relazioni fondamentali tra le funzioni iperboliche
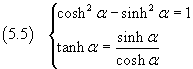
Da queste identità fondamentali si possono dedurne molte altre in modo del tutto analogo a quello seguito per le funzioni trigonometriche circolari.
Sarà sufficiente in questa sede limitarsi a ricavare le uguaglianze che esprimono seno e coseno iperbolici in funzione della tangente iperbolica.
Per il seno
![]()
e, poiché i coseno iperbolico è sempre ≥ 1, quindi sempre positivo
![]()
Analogamente per il coseno
![]()
![]()
Una "rotazione iperbolica" è una trasformazione che trasforma un'iperbole equilatera in sè stessa e quindi lascia invariata l'espressione x2-y2.
Le equazioni di una "rotazione iperbolica" di parametro α sono:
![]()
come si può verificare elevando al quadrato ambo i membri delle due equazioni e sottraendo membro a membro.
Se, estendendo il principio di relatività anche alla luce, si assume che la velocità della luce sia la stessa per due osservatori O e O' in moto relativo uniforme l'uno rispetto all'altro lungo l'asse delle ascisse, bisogna modificare le trasformazioni di Galileo.
Due sistemi di riferimento con origini in O e O' e con gli assi delle ascisse sovrapposti, quando entrambi i loro rispettivi cronometri t e t' segnano 0 hanno anche le origini sovrapposte. L'origine O' si sta muovendo rispetto a O con velocità parallela agli assi delle ascisse, con lo stesso orientamento degli stessi e modulo V.
Nelle considerazioni seguenti ci si riferirà sempre a questa situazione.
Nell'istante in cui le origini sono sovrapposte, quindi nell'istante 0 in entrambi i sistemi, una sorgente luminosa situata nella comune origine, emette un lampo che si propaga come onda sferica avente velocità c in entrambi i sistemi di riferimento.
Nel sistema O la posizione di O' dopo un tempo t è Vt, il raggio del fronte d'onda sferico è r=ct, l'equazione della superficie sferica del fronte è x2+y2+z2=(ct)2 e i punti di tale superficie che si trovano sull'asse delle ascisse sono dati dall'equazione x2=(ct)2, cioè
![]()
Nel piano cartesiano con origine O e assi ortogonali (ct) e x questa equazione è rappresentata da una 'iperbole equilatera' degenerata nella coppia di rette formata dalle bisettrici dei quadranti.
Analogamente per O' i punti del fronte d'onda sull'asse delle ascisse sono dati dall'equazione
![]()
Le trasformazioni cercate devo essere tali che nel passaggio dal sistema di riferimento O al sistema di riferimento O' l'espressione (ct)2-x2 rimanga invariata.
Come s`è visto al paragrafo 5 la trasformazione che lascia invariata la differenza tra i quadrati delle coordinate è la rotazione iperbolica (5.8). In questo caso, nella (5.8), x va sostituito con (ct) e y va sostituito con x: si ottiene
![]()
Nel sistema O, al tempo t, il punto O' ha ascissa Vt; nel sistema O' il punto O' ha sempre ascissa 0 per definizione, quindi, al tempo t', O' ha ascissa 0.
Considerando quindi il punto O' e sostituendo le sue corrispondenti coordinate spazio temporali nella seconda delle (6.3), si ha
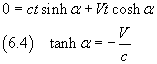
Sostituendo questa espressione della tangente nelle identità (5.6) e (5.7) si ha
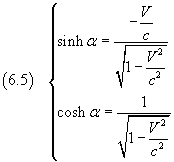
Applicando queste espressioni di coseno e seno iperbolici nelle equazioni (6.3), si ricava
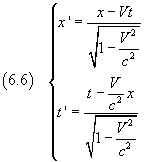
Le (6.6) esprimono le trasformazioni della coordinata x e del tempo t passando dal sistema di riferimento O al sistema di riferimento O'.
Nelle condizioni scelte la y e la z rimangono invariate.
Tali trasformazioni sono note come equazioni di Lorentz ed è necessario sostituirle a quelle corrispondenti di Galileo (2.1) se si vuole che il principio di relatività valga anche per l'ottica e l'elettromagnetismo.
Usualmente il rapporto tra V e c è indicato con β
![]()
Nei movimenti ordinariamente studiati in meccanica classica V è di molti ordini di grandezza minore di c e quindi il rapporto β e, a maggior ragione il suo quadrato, è sperimentalmente indistinguibile da 0. Nelle applicazioni classiche le (6.5) coincidono praticamente con le (2.1).
È pure utile porre
![]()
γ è detto fattore di Lorentz.
Le quattro equazioni di Lorentz possono quindi essere scritte più succintamente nel modo seguente
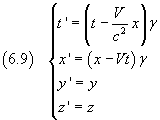
Composizione delle velocità.
Dalle trasformazioni di Lorentz per x e t si può ricavare la relazione tra le velocità corrispondente alla (2.2).
Se nel sistema O un certo punto P ha velocità parallela all'asse delle ascisse, con lo stesso verso e modulo costante v, nel sistema O' il punto P ha velocità di modulo v'
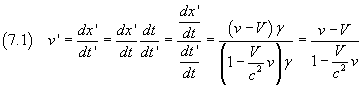
La (7.1) è la legge relativistica di composizione delle velocità che era già stata trovata sperimentalmente da Fizeau.
Se nella (7.1) alla v del secondo membro si sostituisce c, anche a primo membro si ottiene c in accordo con il principio che la velocità della luce è la stessa in tutti i sistemi di riferimento inerziali.
c è un asintoto per le velocità di trascinamento V
La condizione di realtà del radicale che compare nelle trasformazioni di Lorentz impone un importante risultato fisico: qualunque oggetto fisico deve muoversi con velocità inferiore a c.
Contrazione delle lunghezze.
Un'altra importante conseguenza delle trasformazioni di Lorentz è la contrazione delle lunghezze: gli oggetti in movimento sono più corti di quando sono fermi.
La lunghezza di un oggetto fermo rispetto all'osservatore è detta lunghezza propria.
Se nel sistema O' una sbarra parallela all'asse delle x ha lunghezza propria l', in un certo istante t' una estremità di tale sbarra si trova in x'1 e l'altra estremità in x'2, con x'2-x'1=l'.
Nel tempo corrispondente t, l'osservatore O assegnerà alla stessa sbarra la lunghezza l = x2-x1.
Poiché
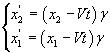
si ha
![]()
e quindi
![]()
cioè la misura della sbarra in O risulta più corta di quanto risulta in O'.
Ad esempio, se per O', che si muove con velocità V=0.5c, la lunghezza della sbarra è l'=10m, per O la lunghezza della stessa sbarra risulta
![]()
Dilatazione dei tempi.
In modo analogo dalle equazioni di Lorentz si desume il fenomeno della dilatazione dei tempi: la durata di un fenomeno misurata da un osservatore O' in moto con velocità V rispetto ad un osservatore O è maggiore della durata della stesso fenomeno misurata da O.
Se nel sistema O la misura della durata T dell'oscillazione di un pendolo appeso ad un punto di coordinata x=0 inizia all'istante t1= 0 e termina all'istante t2=T, allora nel sistema O' la stessa oscillazione ha durata T' che si ottiene dalle (6.6)
![]()
Poiché T' si ottiene dalla divisione di T per un valore minore di 1, risulta T' >T.
Ad esempio, se per O il pendolo ha un periodo di 1s, per O', che si muove con velocità V=0.5c rispetto a O, il periodo del pendolo è
![]()
Una importante verifica sperimentale di questo fatto si ha nella misura della vita media delle particelle subatomiche che si producono in numerose reazioni nucleari.
Ad esempio, se un osservatore O misura la vita media di un pione π fermo rispetto a sé stesso trova un valore di 1.77·10-8 s. Ma se il pione si muove rispetto all'osservatore O con una velocità V=0.9c, la sua vita media, misurata dall'osservatore, risulta 4.06·10-8 s.
Simultaneità
Un'altra conseguenza delle trasformazioni di Lorentz decisamente divergente rispetto all'intuizione ingenua è che, se due eventi sono simultanei per un osservatore, non lo sono per un altro osservatore in moto rispetto ad esso.
Supponiamo che due eventi, nel sistema di riferimento O, avvengano nello stesso istante t sull'asse delle x in due diverse posizioni x1 e x2. In un sistema di riferimento O', per la prima delle (6.9), essi si verificano negli istanti
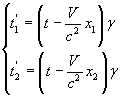
I due eventi sono separati da un intervallo di tempo
![]()
quindi non sono simultanei. Questa osservazione ha importanti implicazioni di carattere epistemologico sulla causalità.
Effetto Doppler relativistico
Vedere Effetto Doppler.
Il fatto che nessun oggetto fisico si possa muovere con velocità uguale o superiore a c non è assolutamente coerente con la meccanica newtoniana.
Per Newton una forza costante di modulo f che agisce su un punto P di massa m imprime su di esso una accelerazione costante di modulo
![]()
e poiché
![]()
data una forza costante, per t→∞, anche v→∞: in un tempo opportuno, P può raggiungere qualunque velocità per quanto alta.
A questo punto sembra chiaro che il secondo principio della dinamica va modificato, e la modifica dovrà essere tale da salvaguardare il fatto che, per quanto a lungo una forza agisca su una particella, la sua velocità finale non arrivi a c.
Per dedurre analiticamente tale risultato conviene enunciare il secondo principio della dinamica nel seguente modo: una forza costante produce una variazione della quantità di moto direttamente proporzionale alla forza stessa e alla durata della sua azione.
La quantità di moto (o momento cinetico) p di un corpo di massa m è espressa dal prodotto della massa per la velocità: p=mv.
![]()
La variazione ΔK dell'energia cinetica K di un corpo libero è data dal lavoro della forza, cioè dal prodotto scalare della forza per lo spostamento subito dal corpo e, poiché forza e lo spostamento siano paralleli ed equiversi, il prodotto scalare si riduce al prodotto dei moduli:
![]()
Gli studi di Planck sulla radiazione di cavità, di Bohr sull'atomo di idrogeno e di Einstein sull'effetto fotoelettrico, hanno dimostrato che l'emissione e l'assorbimento di onde elettromagnetiche avvengono con fenomeni elementari di scambio, da parte di un atomo, di quantità discrete di energia denominate fotoni.
Se si considera un singolo fotone, esso dal momento stesso in cui viene generato, in si muove con velocità costante c, dunque la sua velocità media è c è la sua energia
![]()
La quantità di moto di un fotone risulta quindi
![]()
Einstein propone il seguente esperimento mentale:
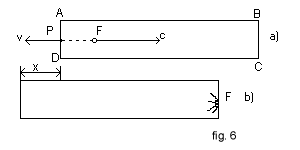
Si considera una scatola a sezione rettangolare ABCD, inizialmente ferma rispetto ad un sistema di riferimento O con asse delle ascisse parallelo ad AB e nel quale il lato AB ha lunghezza propria l0 e la massa della scatola è m0.
Al tempo t=0 (fig. 6a) un punto P sulla parete di sezione AD emette un fotone F verso destra, parallelamente ad AB.
Esattamente come nel caso di un fucile che spara un proiettile, vale il principio di conservazione della quantità di moto: in O la scatola assume una quantità di moto uguale e contraria a quella del fotone, quindi rincula con velocità v verso sinistra desumibile dalla relazione
![]()
dove K è l'energia del fotone e v è il modulo della velocità della scatola dopo l'emissione del fotone.
![]()
Dopo la sua corsa all'interno della scatola, il fotone F urta contro la parete opposta (fig. 6b) e, venendone assorbito, la frena, fermandola.
Quando la scatola è in moto con velocità v, per un osservatore esterno O la sua lunghezza l è, per l'equazione (7.2),
![]()
Sia t il tempo, misurato in O, impiegato dal fotone a raggiungere la parete destra della scatola
![]()
Nello stesso tempo l'estremità sinistra della scatola, e quindi il punto P, si sposta verso sinistra di un tratto di lunghezza x
![]()
Poiché, mentre il fotone è in movimento, la scatola si sposta verso sinistra, lo spazio percorso dal fotone è lo-x, quindi
![]()
Uguagliando le espressioni (8.6) e (8.8) di t si ottiene
![]()
Sostituendo nella (8.7) le espressioni di x, v e t determinate rispettivamente nelle (8.9), (8.5), (8.6), si ottiene
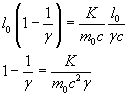
e infine
![]()
La (8.10) è l'espressione dell'energia cinetica di un corpo di massa iniziale m0 che si muove a con velocità di modulo v e deve sostituire la classica
![]()
quando il modulo della velocità v è una frazione apprezzabile di c.
Scrivendo la (8.10) nella seguente forma
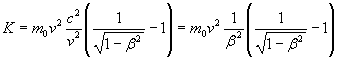
e calcolandone il limite per β→0 si ottiene
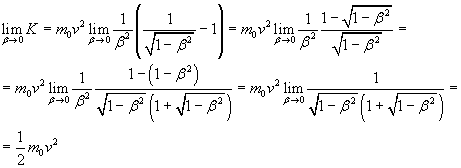
La (8.11), quindi l'espressione classica dell'energia cinetica, è un caso limite dell'espressione relativistica, valida per velocità v molto piccole rispetto a c.
La (8.10) può anche essere scritta
![]()
La (8.12) mostra che l'energia cinetica è data dalla differenza di due termini: il minuendo, che sarà indicato con E, rappresenta l'energia totale posseduta dal corpo alla velocità v; il sottraendo, che sarà indicato con E0, rappresenta l'energia iniziale posseduta dal corpo quando è fermo.
A differenza di quanto teorizzato dalla meccanica newtoniana, un corpo di massa m0 risulta possedere, a riposo, un'energia
![]()
È facile verificare che l'energia totale
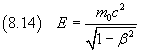
per v=0 coincide con l'energia a riposo.
Se nella (8.14) si pone
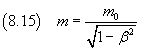
si ottiene l'espressione della massa m in funzione della massa a riposo mo e della velocità v.
Come si vede, al crescere di v la massa aumenta, fino a tendere all'infinito per v che tende a c.
Se nella (8.14) si sostituisce la (8.15) si ottiene quella che sicuramente è la più popolare delle relazioni determinate da Einstein e che può essere considerata il compendio della teoria della relatività ristretta
![]()
Moltiplicando l'espressione della massa (8.15) per v, si ottiene l'espressione relativistica della quantità di moto:
![]()
Ultimo aggiornamento: Giugno 2020